دانلود جزوه ریاضی 1 دانشگاه علوم وفناوریهای نوین گلبهار مشهد

جزوه دکتر جواد صبوری

برای دانلود اینجا را کلیک کنید






برچسب‌ها: جزوه, دانلود, ریاضی1دکتز صبوری, دانشگاه گلبهار
+ نوشته شده در چهارشنبه چهاردهم فروردین ۱۳۹۲ ساعت 3:53 توسط عرفان مرادي  | 

خرید دی وی دی مهندسی معکوس و جزوات

به نام خدا

سلام

بی شک شناخت محصول و درک عوامل موثر در مشخصه های آن، اولین پیش نیاز بهبود کیفیت و نوآوری است که لازمه آن درک مهندسی از مبانی عملکردی قطعه است.

مهندسی معکوس برای بازیابی و تشخیص اجزای متشکله یک محصول بویژه در صورت عدم دسترسی به طراحی اولیه کاربرد داشته و برای نگهداری، گسترش و توسعه امکانات موجود و مهندسی مجدد (RE-ENGINEERING) مورداستفاده قرار می گیرد.

این روش ، روش پذیرفته ای برای کشورهای درحال توسعه به شمار می رود. در این فرایند ابتدا میزان کمبود اطلاعات فنی برای پشتیبانی از تولید یک محصول معین می شود. سپس با انجام یک کار تیمی منسجم، متشکل از متخصصان و محققان رشته های مختلف علوم پایه به همراه مدیریت و سازماندهی مناسب تشکیلات تحقیقاتی و توسعه ای (R&D) سعی می شود مدارک و نقشه های خاص طراحی محصول به دست آید. با درنظر گرفتن مشخصات، هدف و شرایط طراحی محصول، استانداردهای ملی و رایج و همچنین پوشش دادن نقاط مجهول و ناشناخته سعی می شود مراحل نمونه سازی و نیمه صنعتی و در صورت لزوم ساخت و تولید محصول، انجام گردد.

دیگر ریاضی و فیزیک را بدون اطلاعات قبلی بالای 70 در صد بزنید و نگران دروسی مانند عربی کنکور هم نباشید.روانشناسی کنکور در دستان ماست.

برای مثال کافیه یکی از تست هایی رو که بلد نیستید و خیلی وقت می بره رو با مهندس معکوس حل کنید>مثلا

برای حل تست های دامنه  از رشته ریاضی یا رشته های دیگر در درس ریاضی

کافیه بجای قرار دادن تک تک گزینه ها وحل معمولی تست:

اولا یاد بگیرید به جواب ها چطور شک کنید

دوما باید اشترک گزینه ها رو در توابع بررسی و نقاط غیر قابل قبولو مورد سنجش قرار بدید که  کمتر از 30 ثانیه زمان لازمه.حتی اگر تست کارشناسی ارشد هم باشه

می تونم برای ادعای این گزینه شما رو به مجادله وبحث در مورد  هر تستی که شما می گید ببرم

برای خرید دی وی دی مهندسی معکوس و جزوات بعد از  مراجعه به توضیحات بیشتر در ادامه مطلب وخواندن این  موارد با ایمیل زیر تماس بگیرید و یا به شماره زیر پیامک بزنید:

09198720720

erfan_moradi22@yahoo.com

قیمت 50000 ریال

می شود با کنکور کنکور گفتن دهان را به حلاوت  دانشگاه دولتی شیرین کرد


ادامه نوشته
برچسب‌ها: مهندسی معکوس, خرید, فروشگاه, ریاضی
+ نوشته شده در چهارشنبه هجدهم مرداد ۱۳۹۱ ساعت 6:34 توسط عرفان مرادي  | 

عشق به زبان ریاضی

+ نوشته شده در یکشنبه سیزدهم آذر ۱۳۹۰ ساعت 1:20 توسط عرفان مرادي  | 

یک فرمول ریاضی جدید برای تیز هوشان البته با اثبات غلط

به نام او که گر حکم کند محکومیم

چند وقت پیش خودم یه فرمولی رو دتبال می کردم اما نتونستم  به پایان برسونم و فرمول نهایی رو ارائه بدم و فقط به نظریه پردازی نسبت به این فرمول پرداختم.و هر کسی که بتونه فرمول  درستش و واقعی با اثبات کاملشو برام ایمیل کنه بهش یه هدیه می فرستم

مخصوص مبتکران  و متاملان رشته های ریاضی

برای دانلود بر روی عکس زیر کلیک کنید


در پناهش باشید

اللهم صل علی محمد و ال محمد


+ نوشته شده در شنبه بیست و هشتم آبان ۱۳۹۰ ساعت 15:15 توسط عرفان مرادي  | 

فایلی برای دانلود بچه های رشته ریاضی

فایلی برای بچه های رشته ریاضی به صورت پاورپوینت
برای دانلود برروی ادرس زیر کلیک کنید



+ نوشته شده در یکشنبه دوم خرداد ۱۳۸۹ ساعت 2:19 توسط عرفان مرادي  | 

آموزش انتگرال

آموزش انتگرال

انتگرالها يک بحث اساسي رياضيات عالي را تشکيل داده که ميتوان کاربرد آنرا درتمام علوم طبيعي، انساني وغيره مورد مطالعه قرارداد.

اولين بار لايب نيتس نماد استانداردي براي انتگرال معرفي کرد. 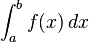\int_{a}^{b} f(x)\, dx aو b نقاط ابتدا و انتهاي بازه هستند و f تابعي انتگرال‌پذير است و dx نمادي براي متغير انتگرال گيري است.

از لحاظ تاريخي dx يک کميت بي نهايت کوچک را نشان مي‌دهد. هر چند در تئوريهاي جديد، انتگرال گيري بر پايه متفاوتي پايه گذاري شده است.

تابع اوليه

هر گاه معادله مشتق تابعي معلوم باشد وبخواهيم معادله اصلي تابع را تعيين کنيم اين عمل را تابع اوليه مي ناميم.

تعريف: تابع اوليه y = f(x)را تابعي مانند Y = F(x) + c مي ناميم،هرگاه داشته باشيم:

cعدد ثابت (y = F(x) + c)' = y = f(x)

انتگرال نامعين

تعريف:هرگاه معادله ديفرانسيلي تابعي معلوم باشد وبخواهيم معادله اصلي تابع را معلوم کنيم اين عمل راانتگرال نا معيين ناميده و آن را با نماد 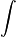\int نمايش مي دهند.

بنا به تعريف نماد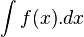\int{f(x)}.dx را انتگرال نامعين ناميده وحاصل آن را تابعي مانندF(x) + c در نظر ميگيريم هر گاه داشته باشيم: 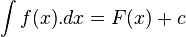\int{f(x)}.dx=F(x)+c با شرط: (F(x) + c)' = f(x)

انتگرال معين

بنا به تعريف نماد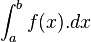\int_a^b f(x).dx را انتگرال معين ناميده و حاصل آن را عددي به صورت زير تعريف ميکنيم: a\int_a^b f(x).dx=[F(x)]_a^b=F(b)-F(a)

aوb را به ترتيب کرانهاي بالا و پايين انتگرال ميناميم.

تابع انتگرال‌پذير

اگر تابعي داراي انتگرال باشد به آن انتگرال‌پذير گويند.

تعبير هندسي انتگرال

از نظر هندسي انتگرال برابر است با مساحت سطح محصور زير نمودار.


نکته! انتگرال نمودار سه بعدي(انتگرال سه گانه)معرف حجم محصور زير نمودار است.

انتگرال يک تابع مثبت پيوسته در بازه (0,10) در واقع پيدا کردن مساحت محصور بين خطوط x=0 , x=10 و خم منحني fx است. aو b نقاط ابتدا و انتهاي بازه هستند و f تابعي انتگرال‌پذير است و dx نمادي براي متغير انتگرال گيري است.

 

انتگرال يک تابع مساحت زير نمودار آن تابع است.

انتگرال گيري

انتگرال گيري به معني محاسبه سطح زير نمودار با استفاده از روشها وقوانين انتگرال گيري است.

1.f تابعي در بازه (a,b) در نظر مي‌‌گيريم. 2.پاد مشتق f را پيدا مي‌‌کنيم که تابعي است مانند f که و داريم: 3.قضيه اساسي حساب ديفرانسيل و انتگرال را در نظر مي‌‌گيريم:


بنابراين مقدار انتگرال ما برابر خواهد بود.

به اين نکته توجه کنيد که انتگرال واقعاً پاد مشتق نيست (يک عدد است) اما قضيه اساسي به ما اجازه مي‌‌دهد تا از پاد مشتق براي محاسبه مقدار انتگرال استفاده کنيم. معمولاً پيدا کردن پاد مشتق تابع f کار ساده‌اي نيست و نياز به استفاده از تکنيکهاي انتگرالگيري دارد اين تکنيکها عبارت‌اند از :


  • انتگرال گيري به‌وسيله تغيير متغير
  • انتگرال گيري جزء به جزء : \int u\, dv=uv - \int v\, du
  • انتگرال گيري با تغيير متغير مثلثاتي
  • انتگرال گيري به‌وسيله تجزيه کسرها

روش هايي ديگر نيز وجود دارد که براي محاسبه انتگرالهاي معين به کار مي‌‌رود همچنين مي‌‌توان بعضي از انتگرال ها با ترفند هايي حل کرد براي مثال مي‌‌توانيد به انتگرال گاوسي مراجعه کنيد.

محاسبه سطح زير نمودار به‌وسيله مستطيل هايي زير نمودار. هر چه قدرعرض مستطيل ها کوچک مي‌شوندمقدار دقيق تري از مقدار انتگرال بدست ميآيد.


انتگرال هايي معين ممکن است با استفاده از روش هاي انتگرال گيري عددي ،تخمين زده شوند.يکي از عمومي‌ترين روش ها ،روش مستطيلي ناميده مي‌‌شود در اين روش ناحيه زير نمودار تابع به يک سري مستطيل تبديل شده و جمع مساحت آنها نشان دهنده مقدار تقريبي انتگرال است. از ديگر روش هايي معروف براي تخمين مقدار انتگرال روش سيمپسون و روش ذوزنقه‌اي است. اگر چه روش هاي عددي مقدار دقيق انتگرال را به ما نمي‌دهند ولي در بعضي از مواقع که انتگرال تابعي قابل حل نيست يا حل آن مشکل است کمک زيادي به ما مي‌‌کند.

جدول كامل فرمول هاي انتگرال

 

 

Rules for integration of general functions

\int af(x)\,dx = a\int f(x)\,dx \qquad\mbox{(}a \neq 0 \mbox{, constant)}\,\!
\int [f(x) + g(x)]\,dx = \int f(x)\,dx + \int g(x)\,dx
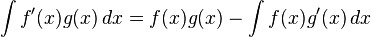
\int f'(x)g(x)\,dx = f(x)g(x) - \int f(x)g'(x)\,dx
\int {f'(x)\over f(x)}\,dx= \ln{\left|f(x)\right|} + C
\int {f'(x) f(x)}\,dx= {1 \over 2} [ f(x) ]^2 + C
\int [f(x)]^n f'(x)\,dx = {[f(x)]^{n+1} \over n+1} + C \qquad\mbox{(for } n\neq -1\mbox{)}\,\!

Rational functions

\int \,{\rm d}x = x + C
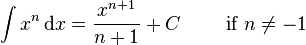
\int x^n\,{\rm d}x = \frac{x^{n+1}}{n+1} + C\qquad\mbox{ if }n \ne -1
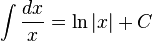
\int {dx \over x} = \ln{\left|x\right|} + C
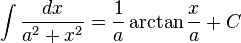
\int {dx \over {a^2+x^2}} = {1 \over a}\arctan {x \over a} + C

Irrational functions

\int {dx \over \sqrt{a^2-x^2}} = \sin^{-1} {x \over a} + C
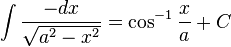
\int {-dx \over \sqrt{a^2-x^2}} = \cos^{-1} {x \over a} + C
\int {dx \over x \sqrt{x^2-a^2}} = {1 \over a} \sec^{-1} {|x| \over a} + C

Logarithms

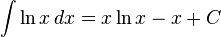
\int \ln {x}\,dx = x \ln {x} - x + C
\int \log_b {x}\,dx = x\log_b {x} - x\log_b {e} + C

Exponential functions

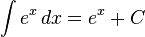
\int e^x\,dx = e^x + C
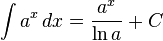
\int a^x\,dx = \frac{a^x}{\ln{a}} + C

Trigonometric functions

\int \sin{x}\, dx = -\cos{x} + C
\int \cos{x}\, dx = \sin{x} + C
\int \tan{x} \, dx = -\ln{\left| \cos {x} \right|} + C
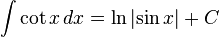
\int \cot{x} \, dx = \ln{\left| \sin{x} \right|} + C
\int \sec{x} \, dx = \ln{\left| \sec{x} + \tan{x}\right|} + C
\int \csc{x} \, dx = \ln{\left| \csc{x} - \cot{x}\right|} + C
\int \sec^2 x \, dx = \tan x + C
\int \csc^2 x \, dx = -\cot x + C
\int \sec{x} \, \tan{x} \, dx = \sec{x} + C
\int \csc{x} \, \cot{x} \, dx = - \csc{x} + C
\int \sin^2 x \, dx = \frac{1}{2}(x - \sin x \cos x) + C
\int \cos^2 x \, dx = \frac{1}{2}(x + \sin x \cos x) + C
\int \sec^3 x \, dx = \frac{1}{2}\sec x \tan x + \frac{1}{2}\ln|\sec x + \tan x| + C
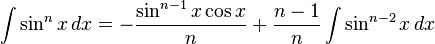
\int \sin^n x \, dx = - \frac{\sin^{n-1} {x} \cos {x}}{n} + \frac{n-1}{n} \int \sin^{n-2}{x} \, dx
\int \cos^n x \, dx = \frac{\cos^{n-1} {x} \sin {x}}{n} + \frac{n-1}{n} \int \cos^{n-2}{x} \, dx
\int \arctan{x} \, dx = x \, \arctan{x} - \frac{1}{2} \ln{\left| 1 + x^2\right|} + C

Hyperbolic functions

\int \sinh x \, dx = \cosh x + C
\int \cosh x \, dx = \sinh x + C
\int \tanh x \, dx = \ln| \cosh x | + C
\int \mbox{csch}\,x \, dx = \ln\left| \tanh {x \over2}\right| + C
\int \mbox{sech}\,x \, dx = \arctan(\sinh x) + C
\int \coth x \, dx = \ln| \sinh x | + C
\int \mbox{sech}^2 x\, dx = \tanh x + C

Inverse hyperbolic functions

\int \operatorname{arcsinh} x \, dx = x \operatorname{arcsinh} x - \sqrt{x^2+1} + C
\int \operatorname{arccosh} x \, dx = x \operatorname{arccosh} x - \sqrt{x^2-1} + C
\int \operatorname{arctanh} x \, dx = x \operatorname{arctanh} x + \frac{1}{2}\log{(1-x^2)} + C
\int \operatorname{arccsch}\,x \, dx = x \operatorname{arccsch} x+ \log{\left[x\left(\sqrt{1+\frac{1}{x^2}} + 1\right)\right]} + C
\int \operatorname{arcsech}\,x \, dx = x \operatorname{arcsech} x- \arctan{\left(\frac{x}{x-1}\sqrt{\frac{1-x}{1+x}}\right)} + C
\int \operatorname{arccoth}\,x \, dx = x \operatorname{arccoth} x+ \frac{1}{2}\log{(x^2-1)} + C

Definite integrals lacking closed-form antiderivatives

\int_0^\infty{\sqrt{x}\,e^{-x}\,dx} = \frac{1}{2}\sqrt \pi 
\int_0^\infty{e^{-x^2}\,dx} = \frac{1}{2}\sqrt \pi 
\int_0^\infty{\frac{x}{e^x-1}\,dx} = \frac{\pi^2}{6} 
\int_0^\infty{\frac{x^3}{e^x-1}\,dx} = \frac{\pi^4}{15}
\int_0^\infty\frac{\sin(x)}{x}\,dx=\frac{\pi}{2}
\int_0^\frac{\pi}{2}\sin^n{x}\,dx=\int_0^\frac{\pi}{2}\cos^n{x}\,dx=\frac{1 \cdot 3 \cdot 5 \cdot \cdots \cdot (n-1)}{2 \cdot 4 \cdot 6 \cdot \cdots \cdot n}\frac{\pi}{2} (if n is an even integer and \scriptstyle{n \ge 2})
\int_0^\frac{\pi}{2}\sin^n{x}\,dx=\int_0^\frac{\pi}{2}\cos^n{x}\,dx=\frac{2 \cdot 4 \cdot 6 \cdot \cdots \cdot (n-1)}{3 \cdot 5 \cdot 7 \cdot \cdots \cdot n} (if \scriptstyle{n} is an odd integer and \scriptstyle{n \ge 3} )
\int_0^\infty\frac{\sin^2{x}}{x^2}\,dx=\frac{\pi}{2}
\int_0^\infty x^{z-1}\,e^{-x}\,dx = \Gamma(z) 
\int_{-\infty}^\infty e^{-(ax^2+bx+c)}\,dx=\sqrt{\frac{\pi}{a}}\exp\left[\frac{b^2-4ac}{4a}\right]
\int_{0}^{2 \pi} e^{x \cos \theta} d \theta = 2 \pi I_{0}(x) 
\int_{0}^{2 \pi} e^{x \cos \theta + y \sin \theta} d \theta = 2 \pi I_{0} \left(\sqrt{x^2 + y^2}\right)
\int_{-\infty}^{\infty}{(1 + x^2/\nu)^{-(\nu + 1)/2}dx} = \frac { \sqrt{\nu \pi} \ \Gamma(\nu/2)} {\Gamma((\nu + 1)/2))}\, (\nu > 0\,,
\int_a^b{f(x)\,dx} = (b - a) \sum\limits_{n = 1}^\infty {\sum\limits_{m = 1}^{2^n - 1} {\left( { - 1} \right)^{m + 1} } } 2^{ - n} f(a + m\left( {b - a} \right)2^{-n} )

\begin{align} \int_0^1 x^{-x}\,dx &= \sum_{n=1}^\infty n^{-n} &&(= 1.291285997\dots)\\ \int_0^1 x^x \,dx &= \sum_{n=1}^\infty -(-1)^nn^{-n} &&(= 0.783430510712\dots) \end{align}

+ نوشته شده در سه شنبه چهاردهم اردیبهشت ۱۳۸۹ ساعت 16:16 توسط عرفان مرادي  | 

آشنایی با کتابهای آنالیز ریاضی

آشنایی با کتابهای آنالیز ریاضی
نام کتاب نویسنده و مترجم
چکیده کتاب
ناشر
اصول آنالیز ریاضی
 

 

 

 

 

 نویسنده: والتر رودین مترجم: دکتر علی اکبر عالم زاده



























کتاب اصول آنالیز ریاضی والتر رودین شهره ی آفاق است. هر کجا دانشگاهی هست و ریاضیاتی، این کتاب و مولف آن مطرح اند. اهل فن این کتاب را بهترین کتاب آنالیز می دانند. این کتاب متنی است برای درس آنالیز و معمولا" به دانشجویان پیشرفته ی دوره ی لیسانس و یا دانشجویان سال اول فوق لیسانس ریاضی پیشنهاد می شود. چاپ اول آنالیز رودین در ایران در سال 1362 صورت گرفته است. در چاپ های بعدی مطالب مربوط به توابع چند متغیره تقریبا" به طور کامل، با توضیحات بیشتر، مثال های افزون تر و انگیزه ی زیادتر، باز نویسی شده اند. برهان قضیه ی تابع معکوس، مطلب مشکل گشای فصل9 ( توابع چند متغیره )، به وسیله ی قضیه ی نقطه ی ثابت درباره ی نگاشت های انقباض، ساده گشته است، فرم های دیفرانسیل به طرز مبسوط تری مورد بحث قرار گرفته اند. چند کاربرد قضیه ی استوکس نیز گنجانده شده اند. شایان ذکر است که کتاب فوق، در 1362، کتاب سال جمهوری اسلامی ایران در رشته ی ریاضی بوده است انتشاموسسه انتشارات علمی دانشگاه صنعتی شریف سال 1372 رات علمی و فنی
آنالیز ریاضی نویسنده: تام م. اپوستل مترجم: دکتر علی اکبر عالم زاده یکی از مشهورترین کتاب های آنالیز سال های اخیر، کتاب آنالیز ریاضی، نوشته ی تام م. اپوستل می باشد. این کتاب درسی مباحث آنالیز را در سطح حساب دیفرانسیل و انتگرال عالی مورد بحث قرار داده است و در آن، موضوع به صورت صحیح، دقیق، امروزی، و در عین حال نه چندان غیر عملی، عرضه گشته و راهی را از حساب دیفرانسیل و انتگرال مقدماتی به دوره های عالی در نظریه ی تابع های حقیقی و مختلط می گشاید و خواننده را با برخی از تفکرات انتزاعی، که در آنالیز نوین متداول است آشنا می سازد.در این کتاب، توپولوژی مجموعه های نقطه ای در محدوده ی فضاهای متری کلی به همان گونه ی فضای n- بعدی اقلیدسی عرضه شده و افزون بر آن دو فصل درباره ی انتگرال گیری لبگ به روش ریس_ناگی وجود دارد که مستقیما" به تابع ها و انتگرال های آن ها توجه شده و از نظریه ی اندازه ها مستقل است. این کتاب در دوره های ریاضیات، در سطوح مختلفی به کار می رود و از آن هم به عنوان یک کتاب درسی و هم به عنوان یک کتاب مرجع تکمیلی استفاده می شود. از فصل های 1 تا 5 و 12 و 13 می توان درسی در حساب دیفرانسیل تابع های یک یا چند متغیره و از فصل های 6 تا 11 و 14 و 15 درسی در نظریه ی انتگرال گیری فراهم ساخت موسسه انتشارات امیر کبیر، سال 1380
آنالیز ریاضی نویسنده: دکتر غلامحسین مصاحب هدف این کتاب آماده کردن محصلین برای تحصیل آنالیز ریاضی است ولی به سبب روش تالیفش که مبتنی بر روش های تعلیمی این عصر در ریاضیات است و ریاضیات جدید الهام بخش آن بوده است، پایه تحصیلی مناسبی برای هر رشته ی دیگر این علم می باشد. در دو مقاله تنظیم شده: مقاله ی اول در مقدمات عمومی و شامل بخش هایی با عناوین: آشنایی با مقدمات، آشنایی با مجموعه ها و نسبت، و مقاله ی دوم در تئوری اعداد حقیقی دارای فصول: اصول موضوعه ی اعداد حقیقی، نتایج اصول موضوعه ی میدان مرتب، اصل موضوع تمامیت، حدود رشته ها، سلسله ها و عدد نویسی و محاسبه. ضمنا" در کتاب مذکور علاوه بر فصل های یاد شده، مباحث گرانقدری راجع به زبان منطق، متمم مبحث مجموعه ها و نسب، ترکیبات، حدود اعلی و اسفل رشته ها، نامساوی های مهم و میدان اعداد مختلط نیز وجود دارد انتشارات آستان قدس رضوی، سال 1369
آشنایی با آنالیز ریاضی نویسندگان: ویلیام ر. پارزینسکی - فیلیپ و. زیپس ، مترجم: سید محمود طالبیان این کتاب برای خوانندگانی در نظر گرفته شده است که قبلا" هیچ بسط نظری و دقیقی از حساب دیفرانسیل و انتگرال را ندیده اند، همچنین مثال های روشنگرانه ی متعددی با توضیحات تفصیلی در آن گنجانده شده است. در فصل های اولیه بعضی از اثبات ها به طرزی توصیفی آمده اند، لذا بصیرت بیشتری در شناخت ساختمان استدلال های ریاضی فراهم و به بسط مهارت های به کار رفته در اثبات گزاره ها در ریاضیات کمک می کند. اکثر تمرینات توانایی محصل در استفاده از روش ها و فنون به کار رفته در متن را طلب می کنند و حل تمرینات باعث ایجاد ادراکی عمیق تر و دقیق تر از قضایا و اثبات آن ها می شود. کتاب فوق الذکر شامل مباحثی از جمله بسط دستگاه اعداد حقیقی، دنباله ها و مجموعه ها، توابع مشتق پذیر، انتگرال ریمان و دنباله ها و سری های توابع است. انتشارات ققنوس، سال 1379
آنالیز عددی نویسندگان: ریچارد ال. بوردن - ج. دوگلاس فیرز - آلبرت سی. رینولدز ، مترجمان: علی اکبر عالم زاده - اسماعیل بابلیان - محمدرضا امیدوار خوانندگان این کتاب عمدتا" دانشجویان سال سوم علوم و مهندسی اند که مبانی حساب دیفرانسیل و انتگرال را دیده و از یک زبان برنامه نویسی سطح بالا، عموما" فرترن، اطلاع دارند. دانستن مبانی نظریه ی ماتریس ها و معادلات دیفرانسیل در بخش های بعدی کتاب مفیدند، لیکن، برای بی نیازی از آنها، به عنوان پیشنیاز مطالب مقدماتی به حد کافی گنجانده شده است. همچنین علاقمندان می توانند انواع مسایل قابل حل به وسیله ی تکنیک های عددی و مشکلات ناشی از این روش ها را بیاموزند. موارد زیر با فلسفه ی کتاب سازگارند: دادن درکی از روش های عددی، چگونه و چرا این روش ها کار می کنند، و حدود کارایی آنها، درکی که پایه ی استوار برای مطالعات آتی یا پذیرش تکنیک های جدیدتری باشد که در آینده طرح می شوند. برای هر روش مهم در متن، یک الگوریتم مشروح بدون ذکر برنامه ای خاص ارایه گشته است. الگوریتم ها به نحوی عرضه شده اند که حتی یک شاگرد با تجربه ی محدود در برنامه نویسی می تواند آن ها را به دستورات برنامه تبدیل کند. بیان این نکته ضروری است که هیچ برنامه ی عملی در متن درس گنجانده نشده است. هر مفهوم آمده در متن کتاب با مثال توضیح داده شده، و بیش از 700 تمرین در آن وجود دارد. این تمرینات از کاربردهای ساده ی الگوریتم ها تا تعمیم ها و توسیع های پیچیده ی نظریه تغییر می کند. به علاوه، تعداد زیادی مساله ی کاربردی از مباحث مختلف مهندسی و علوم فیزیک، بیولوژی و اجتماعی ارائه شده است. مرکز نشر دانشگاهی سال 1364
نظریه و کاربردهای آنالیز عددی نویسندگان: ج.م.فیلیپس – پ.ج.تیلر ، مترجمان: غلامحسین بهفروز – میر کمال میرنیا در فصل های اولیه این کتاب، به منظور یادآوری و پایه گذاری مطالب بعدی، شمه ای از حساب دیفرانسیل و انتگرال گنجانده و بعد از آن مقدمه ی مختصری بر ماتریس ها آورده شده است. مطالب کتاب از ابتدا به روالی منطقی و مستقل، با تاکید برابر بر روش های عملی و نظری ریاضی ارائه، الگوریتم ها دقیقا" بیان، و عموما" اثبات قضایا نیز آورده شده اند و این بسیار مفید واقع می شود چراکه هر یک دیگری را روشن تر می سازد.برای ارائه ی روشی یکسان در سراسر کتاب، تا حد امکان از تقریب ها استفاده گشته. بنابراین، انواع مختلف تقریب هایی که ارائه شده اند، در فصل های مربوط به حل معادلات جبری غیر خطی، انتگرال گیری عددی و معادلات دیفرانسیل به کار می روند. همچنین برای کمک به خواننده در بالا بردن مهارت ها، تعداد زیادی مثال حل شده آمده است. مسائل آخر هر فصل به منظور آزمونی از میزان درک دانشجویان، و کمکی برای توسعه ی مطالب کتاب می باشد.
نخستین گام ها در آنالیز عددی نویسندگان: آر.جی.هوسکینگ – دی.سی.جویس – جی.سی.ترنر ، مترجمان: اسماعیل بابلیان – میر کمال میرنیا هر مبحث اصلی این کتاب به تعدادی گام تقسیم شده است. پنج گام اول به مساله ی خطاهای ناشی از کار عددی اختصاص داده شده است که برای آشنایی صحیح با هنر استفاده از روش های عددی و درک کامل خطاها لازم است. مفاهیم و روش هایی که در مباحث معادلات غیر خطی، دستگاه معادلات خطی، درونیابی، مشتق گیری و انتگرال گیری مورد استفاده قرار می گیرند مربوط به گام های بعدی هستند. در داخل هر گام، ابتدا مفاهیم و روش هایی را که باید فرا گرفته شود، ارائه شده و متعاقبش چند مثال روشن کننده. ضمنا" چند فلوچارت اساسی به صورت یک ضمیمه به کتاب اضافه شده است. مرکز نشر دانشگاهی سال 1366
+ نوشته شده در جمعه ششم فروردین ۱۳۸۹ ساعت 19:10 توسط عرفان مرادي  | 

مقدمه ای جامع بر هندسه دیفرانسیل

+ نوشته شده در جمعه ششم فروردین ۱۳۸۹ ساعت 19:6 توسط عرفان مرادي  | 

رسم توابع در چند ثانیه

+ نوشته شده در جمعه ششم فروردین ۱۳۸۹ ساعت 19:4 توسط عرفان مرادي  | 

آمار و احتمالات

آمار و احتمالات همواره با آزمايش هاي تصادفي درگير هستند. امثال اين آزمايش ها شامل وقوع تصادفات رانندگي ، خطاهاي اندازه گيري ، توليد محصول سالم يا معيوب يك خط توليد و انواع بازي هاي شانسي همچون بيرون كشيدن يك كارت از دسته كارت ها ، پرتاب سكه و پرتاب تاس مي باشد.

مجموعه اي از اصول احتمال گردآوري شده و در قالب PDF قابل دانلود است. موضوعات اين كتابچه عبارتست از:

    1- نظريه مجموعه ها
    2- مفاهيم و تعاريف احتمال
    3- قضاياي پايه اي احتمال

منابع:

[1] راس،شلدون(1994) ،مباني احتمال، ترجمه پارسيان ، همداني، نشر شيخ بهايي – اصفهان 1379

دانلود نسخه قابل چاپ PDF با حجم 117 كيلو بايت

+ نوشته شده در جمعه ششم فروردین ۱۳۸۹ ساعت 18:54 توسط عرفان مرادي  | 

مشتق گیری و مشتق پذیری

مشتق و کاربرد آن 

مشتق گیری و مشتق پذیری :


در گذشته های نه چندان دور، مشتق یک تابع را به صورت زیر نشان می دادند:


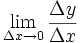
که در این فرمولنشان دهنده میزان تغییرات یک کمیت است. ولی در حال حاضر برای محاسبه مشتق توابع،بیشتر از فرمول زیر استفاده میکنند:


معمولا از نمادهای زیر برای نشان دادن مشتق تابع f نسبت به متغیر x، استفاده میکنند:





یک تابع را در نقطه ای مانند x مشتق پذیر گویند اگردر آن نقطه مشتق موجود باشد. و برای مشتق پذیری تابع در یک بازه لازم است تابع در هر نقطه دلخواه از بازه مشتق پذیر باشد.اگر تابع در نقطه ای مانند c پیوسته نباشد آنگاه در c نمیتواند مشتق پذیر باشد.البته لازم به ذکر است که پیوستگی در یک نقطه وجود مشتق را تضمین نمیکند.مشتق یک تابع مشتق پذیر میتواند خود نیز مشتق پذیر باشد،که به مشتق آن مشتق دوم تابع گویند.مشتق مراتب بالاتر نیز به همین ترتیب تعریف میشوند.

بررسی مشتق از نظر هندسی :

img/daneshnameh_up/1/12/momas22.gif


از نظر هندسی مشتق یک تابع در یک نقطه دلخواه ،شیب خط مماس بر منحنی در آن نقطه است.البته پیدا کردن مستقیم شیب خط مماس در یک نقطه کار دشواری است.زیرا فقط مختصات یک نقطه از خط مماس را داریم.(برای پیدا کردن شیب یک خط از مختصات دو نقطه بر روی خط استفاده میکنیم)برای حل این مشکل از یک خط متقاطع استفاده کرده و این خط را به خط مماس نزدیک میکنیم.برای درک بهتر موضوع به شکل مقابل توجه نمایید.در این شکل خط متقاطع با رنگ بنفش و خط مماس با رنگ سبز مشخص شده است و عددی که در تصویر تغییر میکند نشان دهنده شیب خط متقاطع میباشد. حال از دیدگاه ریاضی این روش را بیان میکنیم:
از دیدگاه ریاضی بدست آوردن مشتق با حد گیری از شیب خط قاطع که به خط مماس نزدیک شده است بدست می آید.پیدا کردن شیب نزدیکترین خط متقاطع به خط مماس با استفاده از کوچکترین h در فرمول زیر حاصل میشود:



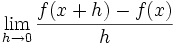
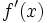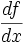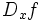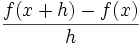
عکس پیدا نشد
بزرگنمایی خط مماس بر یک نقطه روی خط

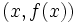در این فرمول h به عنوان کوچکترین تغییر متغیر x تعریف میشودو میتواند مقدار مثبت یا منفی اختیار کند. در این فرمول شیب خط با استفاده از نقاط و 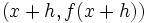حاصل میشود.واضح است که در این روش فقط یک نقطه روی خط برای ما معلوم است و نیازی برای بدست آوردن نقطه دوم روی خط وجود ندارد.همچنین در این روش مشتق x ،حاصل حد زیر است:



ارتباط مشتق با علم فیزیک :

مشتق نقش مهمی در تعریف برخی ار کمیتهای فیزیک حرکت دارد.ما با داشتن موقعیت اجسام بر حسب زمان میتوانیم سرعت و شتاب آنها را محاسبه کنیم.اگر ما از معادله مکان جسم بر حسب زمان مشتق بگیریم معادله سرعت بدست میآید و اگر از معادله سرعت مشتق گیری نماییم(مشتق دوم معادله مکان)معادله شتاب حاصل میشود.

نقاط بحرانی :

نقاطی از تابع که به ازای آنها مشتق تابع تعریف نشده و یا برابر صفر باشد را نقاط بحرانی مینامند.اگر مشتق دوم در یک نقطه بحرانی مثبت باشد،آن نقطه مینیمم نسبی است.و اگر منفی باشدماکزیمم نسبی است،و اگر برابر صفر باشد ممکن است ماکزیمم و مینیمم نسبی نباشد.مشتق گرفتن و بدست آوردن نقاط بحرانی،اغلب ساده ترین راه برای پیدا کردن مینیمم و ماکزیمم نسبی است.(دربهینه سازی نیز این روش بسیار مفید است.به طور کلی مینیمم و ماکزیمم نسبی فقط میتوانند جزئ نقاط بحرانی باشند.

تجزیه و تحلیل نمودارها :

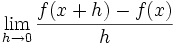
مشتق ابزار مناسبی برای آزمودن نمودار تابع است. نقاطی از دامنه تابع که به ازای آنها مشتق اول برابر صفر شود میتوانند نقاط اکسترمم نسبی تابع باشند.البته باید توجه کرد که تمام نقاط بحرانی نقاط اکسترمم نسبی نیستند.برای مثال تابع 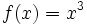یک نقطه بحرانی در x=0 دارد، ولی میتوان از نمودار تابع متوجه این نکته شد که تابع در این نقطه دارای ماکزیمم یا مینیمم نسبی نیست.
آزمون مشتق اول و آزمون مشتق دوم ، روش هایی را برای تشخیص نقاط ماکزیمم و مینیمم نسبی فراهم میکند.لازم به ذکر است در فضاهای چند بعدی نقاط اکسترمم را با استفاده از مشتقات جزئی بدست میآورند.

 

رسم خم با استفاده از مشتق اول:

وقتی بدانیم که تابعی در هر نقطه از بازه‌ای مشتق دارد، بنابر قضایای مشتق خواهیم دانست که تابع در سراسر آن بازه پیوسته است و نمودارش در آن بازه قطع شدگی ندارد. مثلا نمودارهای توابع مشتقپذیر y=Sin x همانند نمودار چند جمله‌ایها ، هر چه ادامه بیابند قطع نمی‌شوند. نمودارهای y = tan x و y = 1/x2 صرفا در نقاطی که توابع مربوط تعریف نشده هستند قطع می‌شوند. بر بازه‌ای که این نقاط را شامل نباشند توابع مزبور مشتق پذیرند؛ و بنابراین پیوسته‌اند و نمودارهایشان قطع شدگی ندارد. اگر بدانیم مشتق تابعی کجا مثبت و کجا منفی و کجا صفر می‌باشد، آنگاه می‌توانیم درباره شکل نمودار آن تابع اطلاعاتی بدست آوریم. با دانستن این مطلب می‌توان مشخص کرد که نمودار در کجا بالا می‌رود ، پایین می‌آید یا مماس افقی دارد.

تایعی چون (y = f(x را سراسر یک بازه Iصعودی می‌گویند. هرگاه با افزایش y , x هم زیاد شود ؛ و در سراسر I نزولی گویند هرگاه با افزایش x و y کاهش یابد. وقتی x در I از چپ به راست حرکت می‌کند نمودار یک تابع صعودی ، خیز بر می‌دارد و نمودار یک تابع نزولی افت می‌کند. صعود یک تابع با مشتقهای مثبت همراه است و نزول تابع با مشتقهای منفی. بنابراین اگر ´f در هر نقطه از یک بازه I مثبت لاشد آنگاه f بر I صعود می کند. و اگر ´f در هر نقطه I منفی باشد، آنگاه f بر I نزول می‌کند. این واقعیتها را به عنوان آزمون مشتق اول برای صعودی و نزولی بودن می‌پذیریم. آزمون مشتق اول به زبان هندسی حاکمی است که توابع مشتقپذیر بر بازه‌هایی صعود می‌کنند که نمودارشان شیب مثبت داشته باشند و بر بازه‌هایی نزول می کنند که نمودارشان شیب منفی داشته باشند.

مماسهای افقی:

از آنجا که مشتقی چون ´f در هر بازه I یی که َf تعریف شود دارای ویژگی مقدار میانی است، هر وقت ´f در این بازه تغییر علامت می‌دهد، باید مقدارش صفر شود. پس هر وقت َf در بازه I تغییر علامت می‌دهد نمودار f باید مماس افقی داشته باشد. اگر وقتی x از چپ به راست می‌رود و از نقطه‌ای چون C می‌گذرد، مقدار ´f از مثبت به منفی تبدیل شود، آنگاه مقدار f در c یک مقدار Max موضعی f است. به همین ترتیب اگر وقتی x از از چپ به راست حرکت می‌کند و از نقطه‌ای چون d می‌گذرد. مقدار ´f از منفی به مثبت تبدیل شود. مقدار f در d یک مقدار Min موضعی f است. *نمی‌توان گفت که هر وقت مشتق صفر شد الزاما تغییر علامت در نمودار تابع ایجاد می‌شود، بنابراین گاهی اوقات در حالی که Min , Max وجود ندارند مماس افقی وجود دارد، مثل تابع y = x3 با اینکه y´= 3x2 در مبدأ صفر است و در هر دو طرف مثبت است. با این همه مماس افقی y=0 نمودار y = x3 را در مبدأ قطع می‌کند.

تقعر و نقطه عطف:

در این قسمت چگونگی رسم دقیق‌تر نمودار با استفاده از علامت مشتق دوم تابع را تشریح می‌کنیم. همان طور که می‌دانیم تابع y = x3 (برای خودتان رسم کنید) همراه با افزایش x صعود می‌کند. اما قسمتی از خم که مربوط به بازه (0, ∞-) و قسمت مربوط به (∞و0) در جهتهای متنفاوتی می‌پیچیند، اگر در امتداد خم از سمت چپ به طرف مبدأ برویم پیچش خم به سمت راست است. وقتی از مبدأ دور می‌شویم، خم به سمت چپ می‌پیچد. توصیف پیچش به طریق دیگر این است که وقتی نقطه تماس از سمت چپ به مبدأ میل می‌کند مماس بر خم در جهت ساعت می‌چرخد، در این حالت شیب خم تقلیل می‌یابد. وقتی نقطه تماس از مبدأ وارد ربع اول می‌شود، مماس در خلاف جهت ساعت می‌چرخد. در این حالت می‌گوییم شیب خم زیاد شده است. بنابراین برای یافتن روی تقعر توسط مشتق باید بگوییم در بازه‌ای که ´y کم می‌شود تقعر رو به پایین دارد و در بازه‌ای که ´y زیاد می‌شود تقعر رو به بالا دارد. توسط آزمون مشتق دوم می‌توانیم بگوییم در نمودار (y = f(x ، در بازه‌ای که مشتق دوم y کوچکتر از صفر باشد، تقعر رو به پایین دارد. در بازه ای که مشتق دوم y بزرگتر از صفر باشد، تقعر رو به بالا دارد.

کاربرد نقطه عطف در رسم توابع :

نقطه‌ای از خم که در آن تقعر عوض می‌شود نقطه عطف داریم. پس نقطه عطف خمی که دو بار مشتق پذیر است نقطه‌ای است در یک طرفش مثبت و در طرف دیگرش منفی است و خود مشتق دوم y در نقطه عطف مقدار صفر دارد. البته ممکن است مشتق دوم y در نقطه‌ای که عطف نیست صفر باشد. همچنین ممکن است نقطه عطف در جایی باشد که مشتق دوم y وجود نداشته باشد.

مجانبها و تقارن :

در این قسمت توابع گویا از x را با در نظر گرفتن رفتارشان ، وقتی مخرج به صفر نزدیک یا x از لحاظ عددی بزرگ می‌شود، بررسی می کنیم. نمودار تابع های زوج وفرد تقارنهایی دارند که آگاهی از آنها برای ترسیم نمودارشان مفید و مهم است.

  • باید این را بدانیم که نمودار توابع زوج نسبت به محور yها متقارن است و نمودار توابع فرد نسبت به مبدأ مختصات متقارن می‌باشد.

مجانبهای افقی و قائم :

وقتی یک نقطه p روی نمودار تابعی چون (y = f(x رفته رفته از مبدأ دور می‌شود، ممکن است فاصله بین p و خطی ثابت به صفر نزدیک شود؛ به عبارت دیگر ، خم وقتی از مبدأ دور می‌شود به خط میل کند. در این حالت ، خط را مجانب نمودار می‌نامند.


خط y = b مجانب افقی نمودار (y = f(x است اگر داشته باشیم: حد تابع (y = f(x وقتی که x به سمت بینهایت و یا منفی بینهایت میل می‌کند برابر با b شود.


خط x = a مجانب قائم نمودار تابع است، اگر داشته باشیم: حد تابع (y = f(x وقتی که x به سمت a- و یا a+ میل می‌کند برابر با ∞± شود.

مجانب مایل :

اگر تابع گویایی خارج قسمت دو چند جمله‌ای باشد که عامل مشترک نداشته باشند و اگر درجه صورت ، یک واحد از درجه مخرج بیشتر باشد، آنگاه نمودار یک مجانب مایل دارد. و بطور کلی برای رسم نمودار یک تابع باید مجانبها ، تقعرها ، نقاط عطف ، مماسها ، نقاط اکسترمم باید مشخص باشند.

کاربردها :

رسم توابع مورد بحث ما در جاهای بسیار وسیع کاربرد دارد. برای مثال پرتاب یک موشک یا یک سفینه با بدست آوردن توابع مربوط و رسم نمودار آ«ها توسط کامپیوتر قبل از عملیات پرتاب توسط مهندسین مورد بررسی قرار میگیرد تا نحوه حرکت و سایر موارد مو شکافی گردد. در ستاره شناسی ، مکانیک ، شیمی و حتی علوم انسانی رسم نمودار توابع از ارزش اجتناب ناپذیری برخوردار است.

اکسترمم: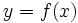

اگر تابع در فاصله ی تعریف شده باشد، آنگاه نقطه ی از نقاط داخلی این فاصله رایک نقطه ی ماکزیمم (یا یک نقطه ی مینیمم) تابع 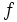گویند، اگر همسایگی این نقطه مانند وجود داشته باشد به طوری که برای هر در این فاصله، نامساوی (یا ) برقرار باشد. نقاط ماکزیمم و مینیمم تابع را نقاط حد نهایی یا نقاط اکسترمم تابع می گویند.


 

شرط لازم وجود اکسترمم :

در نقاط اکسترمم مشتق صفر است و یا وجود ندارد.
توجه: نقاطی که در آن ها یا وجود نداشته باشد را نقاط بحرانی گویند.


 

شرط های کافی وجود اکسترمم :

  1. چنانچه تابع در همسایگی از پیوسته باشد:
    1. اگر وقتی ، و وقتی ، (یعنی زمانی که از طرف چپ به طرف راست نقطه ی حرکت کنیم، علامت مشتق از مثبت به منفی تبدیل شود)، آنگاه نقطه ی ماکزیمم است.
    2. اگر وقتی ، و وقتی ، (یعنی در حرکت از طرف چپ به طرف راست نقطه ی ، علامت مشتق از منفی به مثبت تبدیل شود)، آنگاه را نقطه ی مینیمم گویند.
    3. اگر علامت مشتق در دو طرف نقطه ی ثابت بماند، آنگاه این نقطه اکسترمم نیست.
  2. چنانچه تابع در نقطه ی بحرانی دوبار مشتق داشته باشد، اگر ، آنگاه تابع در نقطه ی ماکزیمم دارد و اگر ، آنگاه مینیمم تابع است ولی اگر ، در این حالت موجودیت اکسترمم در نقطه ی مذکور معلوم نیست.
  3. جنانجه ولی ، اگر زوج باشد، آنگاه وقتی تابع در ماکزیمم است و وقتی تابع در این نقطه مینیمم است. حال اگر فرد باشد، آنگاه در نقطه ی اکسترمم وجود ندارد.
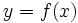  4. چنانچه تابع با معادلات پارامتری مشخص شده باشد که در آن در فاصله ی تغییرات متغییر 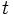مشتقات مرتبه ی اول و دوم دارند و ، به علاوه در ، آنگاه:
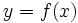    1. اگر آنگاه تابع در ماکزیمم دارد.
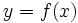    2. اگر آنگاه تابع در مینیمم دارد.
    3. اگر ، در این حالت موجودیت اکسترمم در این نقطه معلوم نیست.

محاسبه ی بیشترین و کمترین مقدار تابع :

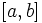بیشترین (یا کمترین) مقدار تابع پیوسته ی در فاصله ی یا در نقاط بحرانی و یا در نقاط انتهایی فاصله است. برای تعیین بیشترین (یا کمترین) مقدار تابع، مقدار آن در تمام نقاط بحرانی واقع در فاصله ی 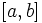، و مقادیر را حساب می کنیم و سپس بیشتری (یا کمترین) مقدار بین آن ها را انتخاب می کنیم.
اگر فاصله ای که تابع در آن تعریف شده است فاصله ی باز باشد، ممکن است تابع بیشترین (یا کمترین) مقدار نداشته باشد.

+ نوشته شده در جمعه ششم فروردین ۱۳۸۹ ساعت 18:53 توسط عرفان مرادي  | 

برترین جزوه حسابان وریاضی2 استان

توجه......................................................................................توجه
برترین جزوه حسابان وریاضی2
سلام .امروز یک جزوه حسابان با ریاضی 2پیدا کردم کهنمونش کمتر یدا میشه .این جزوه دست نویسه وهر کدام یعنی حسابان1وحسابان 2تنها70000ریال است که دست نویس می باشد.


(شما تماس بگیرید با هم را میایم)تلفن خرید:09387384316
.
.
.
.
جزوه ومجموعه کتب تست المپیاد ریاضی دانشگاه واترلو کانادا  ومجموعه ی کامل اموزش ازمون والپیاد ورودی به دانشگاه  واترلو کانادا تنها هر جزوه با تخفیف33%با قیمت 250000ریال
تلفن خرید:(عرفان مرادی)
09387384316
.
.
.
+ نوشته شده در دوشنبه هفدهم اسفند ۱۳۸۸ ساعت 4:2 توسط عرفان مرادي  | 

M a t h e m a t i c a l   j o k e s

How old were they ?

Two students-mathematicians, having birthdays on the same day, wished each other many happy returns on this day.  One of them said:
- You’ll have such birthday only in 11 years.
The other answered him:
- Okay, but you’ll have such birthday only in 96 years.
Both of them were satisfied with each other. How old were they on this day ?


S o l u t i o n.   One of them was 25, and other 24.  Why?
                        25=52, the next square is 62=36, i.e. in 11 years.
                        24=4!, the next factorial is 5!=120,  i.e. in 96 years.


New laws of arithmetic

A pupil divides 28 by 7 and receives as a result 13. His teacher asks him:
- How did you receive this result ?  
- First I divide 8 by 7 and receive 1. Now 1 x 7 = 7 and I write:

                                 

Now I divide 21 by 7 and receive 3. Now I write:

                                 

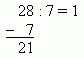
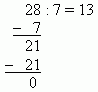
The teacher asks him to check the result by multiplication. The pupil answers:
- I execute 13 x 7  by the steps:
   1)   1 x 7 = 7,
   2)   3 x 7 = 21,
   3)   7 + 21 = 28.

The teacher asks him to check the result by addition. The pupil answers:
- First I add 3 seven times and receive 21, then I add 1 seven times and receive 28.


About application of mathematics in linguistics

A teacher of English was ill and a teacher of mathematics replaced him. He began to compose a table of irregular verbs:

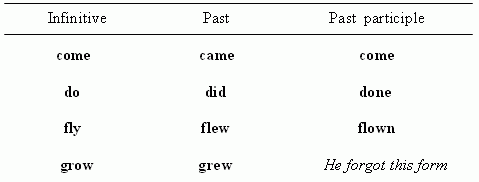
Then he said:
- Okay, I mark this form as  x . Then it’s possible to compose the proportion:

 

 

 

 

 

 

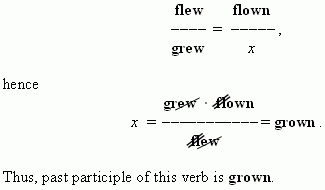
Why do we hear a clatter of train wheels ?

Answer:   Wheel has a form of a circle. An area of a circle is equal to p r 2, so this square clatters.

 

What difference between physicist and programmer ?

Answer:   Physicist thinks that 1 kilobyte = 1000 bytes, and programmer thinks that 1 kilometer = 1024 meters.

 

The shortest distance between two points

At a geometry lesson a teacher asks to represent the shortest distance between the two points A and B on a blackboard: 

 

 

 

 

 

 

The teacher asks:
- Johnny, who taught you this ?
- My father, he is a taxi driver

Sequence

Continue the sequence:    z,  o,  t, … .

S o l u t i o n .  As  z = zero,  o = one,  t = two,  the continued sequence is:

                           z, o, t, t,  f,  f,  s,  s,  e,  n,  t, …

 

At the parents’ meeting

At the parents’ meeting a teacher of mathematics complains of his pupils to their parents:
- Your children are very dull. Today I explained them a new theorem. I explained once, they didn’t understand. I explained
  once again, they didn’t understand. I explained the third time, I understood myself, but they still didn’t understand.

 

Proof

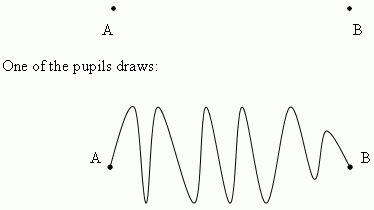
At a geometry lesson a teacher asks to draw an isosceles triangle. One of the pupils draws it. The teacher:
- Now prove that this triangle is really isosceles.
- Sir, I give you a word of a gentleman.

 

Daily time-table

One absent-minded professor composed a daily time-table and showed it to his assistant. The assistant looked it through and said:
- Very well, but your day consists of  25 hours.
- What a pity! Now I must wake up one hour earlier.

 

New about limits

At a mathematics exam a professor asks a student to calculate the limit:



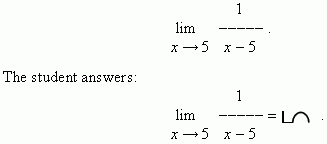
The professor is surprised:
- What is it ? Why ?
The student answers:
- You explained at your lecture that

                                 

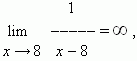
and I have used this example.

 

The shortest telegrams in a history

German mathematician Dirichlet was very taciturn. When his son was born, he sent to his father-in-law the following telegram: “2 +1 = 3”. Maybe it’s one of the shortest telegrams in the history. But the shortest telegram conversation ever was between Oscar Wilde and his publisher regarding his new book. O. Wilde wired the single character “?” and received from his publisher the reply: “!”. 

 

New in chemistry

At a chemistry exam a professor asks a student:
-  Tell me please, how to get sulphur.
The student answers:
-  Let’s take hydrogen sulphide and warm it up. Hydrogen evaporates and sulphur remains.
-  Very well. I put you an “excellent” and warm it up.  A “good” and a “fair” evaporate and  a “poor” remains.

 

Euclid’s wisdom

Euclid was asked:
-  What do you want: two whole apples or four halves ?
-  Four halves, of course.
-  Why ? It’s the same, isn’t it ?
-  No, it isn’t. Choosing two whole apples, I can not see if they are maggoty or aren’t. 

 

Leibniz’s bust

Friends of Leibniz gave him as a present his bust, made by famous sculptor, on his birthday. Leibniz stared at the bust for a long time and then said:
-  So, this is a face, which I shave every day.

 

Einstein and telephone

One woman asked Einstein to remember her telephone number: 361-343.
Einstein answered:
-  It’s very easy. 19 squared and 7 cubed.

 

Einstein at school

A teacher of algebra said to Einstein’s father:
-  I have never met a duller child.

 

An honest sergeant

A sergeant teaches young soldiers:
-  Water boils at 90 degrees.
One of the soldiers retorts:
-  I’m sorry, sir. But I know that water boils at 100 degrees.
-  Okay, I’ll check, - the sergeant answered.
The next day the sergeant says:
-  You were right. Water boils at 100 degrees, I mixed up with a right angle.

 

New method of fast calculus

Two Englishmen are going by train. A conversation isn’t getting on. The train passes a meadow, on which a herd of cows pastures. One of the passengers says:
- 1356.
The other man is surprised, but gives no answer. In some time the train passes another pasture. The first passenger says:
- 1693.
His neighbor brakes and asks:
- Sir, our train moves at speed 60 miles per hour. How can you count so quickly ?
- Oh, sir, it’s very simple! First I count a quantity of legs in a herd and then I divide this number by four.

 

Study and money

Father writes a letter to his son-student:
“Dear John!
I send you 50 dollars, as you asked. By the way remember please that the number 50 is written with one zero, but not with two.”

About terrestrial gravity

A sergeant explains to young soldiers a gist of Earth gravity:
-  If to throw a stone upwards, then it drops to the ground. This means, that the terrestrial gravity effects it.
One of the soldiers asks:
-  What if it drops into water?
-  It doesn’t refer to us. This problem is considered by fleet.

 

At exam

An examiner asks a student:
-  What is your name ?
-  John Smith, sir.
-  Why do you smile ?
-  I’m satisfied with my answer for the first question.

 

An excellent work

A teacher returns a pupil his work:
-  Not a single mistake was made! Johnny, tell me honestly, did anybody help your father ?

 

Valid reason

A teacher asks a pupil:
-  Why does your father make home tasks for you every day ?
-  Because my mother is always busy.

 

Study, sonny

-  Dad, I’m expelled from the college.
-  Don’t weep, I’ll buy you a new college.

 

School’s news

-  Were you asked at school today ?
-  Yes, I was.
-  What about ?
-  Why are you always absent at the parents’ meetings ?

 

Business-like conversation

-  Uncle Bill, I need to tell you something.
-  Well, but tell briefly and clearly.
-  100 dollars, please.

 

General disaster

Two boys went to a doctor.
-  What do you complain about ? – the doctor asks.
-  I swallowed 50 cents. – one of  the boys answered.
-  And why do you weep ? – the doctor asks the other boy.
-  This is my money.

 

Fast calculation

A teacher asks:
-  Tommy, find please a sum of these two numbers.
-  But I didn’t lose it, sir.

 

About inertia

-  Johnny, give an example of inertia.
-  A car has stopped, but a driver is going farther.

                                -------

-  What is an inertia force ?
-  A ball is flying to a window and it’s impossible to catch it.

 

An essence answer

At an arithmetic lesson a teacher asks:
-  How many will it remain, if to subtract 1 from 100 ?
-  Two zeros.

 

Fast solution

A teacher of mathematics writes an equation on a blackboard and calls a pupil:
-  Billy, find  x  please.
-  I have found, here it is! – the pupil answers and shows to  x  with a finger.

 

Working week

-  A cow gives 20 liters of milk a day. How many liters of a milk is it possible to get for a week ?
-  But we don’t know, how many days a week a cow works.

 

Physics news

As it’s known, the famous Albert Einstein tried to solve the problem of time-space unity during last twenty years of his life and didn’t solve it. However this problem was solved recently by sergeant Brown. He drew up a platoon of soldiers and ordered them to dig a ditch from fence till dinner hour.

 

New in geometry

-  How is the biggest side in a right-angled triangle called ?
   As all the pupils keep silent the teacher begins to help:
-  Hy-po-…
-  Hippopotamus !

 

New definition of fraction

A teacher of mathematics:
-  If to take one tomato and to cut it by 4 parts, then each lobule is one fourth part of a tomato. Now do you understand what is a fraction ?
-  Yes, it is a part of salad !

Eureka !

- … And then Archimedes jumped out of a bath and exclaimed:
“Eureka!” – a pupil reads.
-  What is “eureka” ? – a teacher asks.
-  “Eureka” means “he found”.
-  Well. Now tell me please, what Archimedes found in a bath.
-  I think, he found soap.

 

Twice guilty

A pupil tells his comrade:
-  Yesterday my father punished me twice.
-  Why ?
-  The first time he punished me when I showed him a diary and the second time, when the father understood that this was
  his old diary.

 

Beautiful present 

-  Uncle Bill, thank you very much for the trumpet, that you gave me as a present.
-  Do you like the trumpet, Teddy ?
-  Of course! Mother pays 3 dollars to me not to play in the day-time, and my father pays 5 dollars to me not to play in the evening.

 

At exam

An examiner:
-  Why do you wink at me ?
A student:
-  Professor, I signal you that my knowledge is coming to an end.   

                                              -------

An examiner:
-  What do you want: one difficult question or two easy ones ?
-  One difficult, professor.
-  Okay, tell me please, where the first people appeared.
-  In London, sir.
-  Why in London ?
-  I’m sorry, professor, but this is already the second question.

 

Wonders of technical progress

A sergeant bought an electronic watch. A boy comes up and asks him:
-  Tell me please, what the time is.
-  Twelve, divided by thirty one.
-  What does it mean ?
-  Go away, boy. I have been dividing myself for half a day already.

 

Foreseeing monkey

Two monkeys are dismantling an atom bomb.
-  I’m afraid it will blust. – says one of them.
-  Don’t worry, I have another one.

 

Business-like conversation

-  Uncle Bill, I need to tell you something.
-  Well, but tell briefly and clearly.
-  100 dollars, please.

 

Foreseeing cow

A crow flies and sees that a cow climbs up a birch. The crow asks:
-  What are you doing?
-  I want to eat apples. – the cow answers.
-  Are you fool ?  Do you know that apples don’t grow on birches ?
-  Never mind, I have taken them with me.

 

If logic is week …

One man asks his friend:
-  John, tell me please, haw many cakes you can eat on an empty stomach.
-  Five, I think.
-  This is wrong. If you eat only one cake, then the others won’t be on an empty stomach. 
-  This is very interesting puzzle. I’ll tell it my wife.
At home John asks his wife:
-  Tell me please my darling, haw many cakes you can eat on an empty stomach.
-  Six, maybe seven.
-  Oh, what a pity! If you said “five” I could play a practical joke at you.

 

New decimal numeration

-  Tell me please, Billy, how many zeros are written in one million.
-  Six, sir.
-  Well, and how many zeros are written in half-million ?
-  Three, sir.

 

Revenge

A pupil runs to a policeman:
-  Go with me, but quickly!
-  What has happened ?
-  Our teacher has parked his car in a forbidden place.

 

What a speed !

A policeman fined a woman who drove at the speed 100 kilometers per hour! She was very surprised:
 - It’s impossible! I have never heard that so many kilometers could be in one hour!

                                       -------

A policeman stops a driver-disturber:
-  Why are you going at the speed 120 kilometers per hour ?
-  Hour ? – the driver is surprised. – I drive only 15 minutes!

                                       -------

Two friends go by car at the speed 160 kilometers per hour.
- What a speed! And what will happen to us, if a wheel flies off ?
-  Don’t worry! I have a spare wheel.

 

On entrance exams in military academy

An examiner:
-  Captain, solving this equation, you have received that this sine is equal to 4!
    Don’t you know that it’s impossible ?
-  Sir, a value of sine can achieve 4 in wartime!

                                       -------

-  Tell me please, major, what an ellipse is.
-  Ellipse is a circle, inscribed in a square with the sides 2 and 4.

 

Resourceful pupil

At a geography lesson. A teacher asks:
-  Teddy, imagine please that you look northward. What is behind you ?
-  My back, sir.
Gentleman and camel

Gentlemen bought a camel. A seller said to him that the camel knew the three commands: “Phew!” – go,  “Hi!” – run, “Amen!” – stop. Gentleman said: “Phew!” and the camel went, then he said : “Hi!” and the camel ran. Suddenly the gentleman saw that the camel ran toward a precipice, but he forgot how to stop the camel. Understanding that his death was inevitable, he began to pray and said at the end of the prayer: “Amen!”. The camel stopped on the precipice edge. The gentleman wiped sweat from the forehead and said: “Phew!”.

 

How to divide lambs ?

Three friends went to a sage and asked to judge them. They bought together 18 lambs. The first man paid a half of the whole cost, the second – a third and the last – 1 / 9 of the whole cost. They wanted to divide the lambs, but so that all the lambs were alive. The sage said to them: “I can judge you, but I want to get one of the lambs as a reward”. The men agreed. Then the sage gave 9 lambs to the first man, 6 lambs – to the second man, 2 lambs – to the last man andtook 1 lamb for himself. As a result all of them were satisfied. What was a cause of the situation ?


S o l u t i o n.  A cause of this situation was that these three men paid:

1 / 2  +  1 / 3  +  1 / 9  = 17 / 18

                    of the whole cost, i.e. they paid only for 17 lambs, but not for 18.
                    Thus, a seller of the lambs actually presented 1 lamb to the sage.
                    He got the loss, because he didn’t know to count. 

 

Land of total mathematics

In the middle of the XX century Russia was a country, where all people knew mathematics perfectly. In 1965 one newspaper wrote: ”Do you know that a cost of 0.25 liter of vodka, raised to the power, equal to a cost of 0.5 liter of vodka is the number  p with accuracy of three first digits ?”. You can convince in this fact yourself, if to consider that a bottle of 0.25 liter of vodka cost 1.49 ruble, and a bottle of 0.5 liter of vodka cost 2.87 ruble in 1965. Check!

 

Zenonian paradox

Achilles runs after a turtle. Achilles’ velocity is 10 times more than turtle’s velocity. First moment the distance between them is equal to100 m. Achilles runs these 100 m, a turtle creeps 10 m. Achilles runs this 10 m, a turtle creeps 1 m. Achilles runs 1 m, a turtle creeps 0.1 m. Achilles runs 0.1 m, a turtle creeps 0.01 m, and so on. Hence, Achilles will never catch up a turtle ! Explain, please this paradox, known as Zenonian one.


S o l u t i o n.   A cause of this paradox consists in dividing continuous time into
                      parts. We consider smaller and smaller time intervals and receive
                      the paradox as a result. Actually, Achilles will outrun a turtle,
                      of course! Assume that Achilles runs 100 m in 10 seconds, then
                      in next 10 seconds he will run else 100 m, and a turtle will creep
                      this time only 20 m.

 

Generous host

Once a group of 8 guests was taking seats around a big table in a restaurant during a long time. An owner watched this and then said that he agreed to feed them gratis on condition that they would take seats newly every day. How long will he feed them gratis on this condition ?


S o l u t i o n.   This is a classic problem of theory of combinations. Each combination
                      of guests around a table is a permutation, so the number of all
                      possible permutations is equal to

                                            8! = 40320 days ≈ 110 years.

                     Thus, the owner agrees to feed them gratis for 110 years!.

 

Wonders of calculus

Two friends meet. One of them says:
-  Yesterday I was in a circus and saw a trained boa. His length is 8 meters from a head to a tail and 9 meters from a
    tail to a head.
-  It’s impossible!
-  Why? Don’t you know that from Monday to Sunday there are 7 days, and from Sunday to Monday there is only 1 day.

 

Weather forecast

London. Midnight. It’s raining. Can one believe in a weather forecast, that in 72 hours a weather in London will be sunny ?


S o l u t i o n.   No, one can’t, because in 72 a midnight will be again, and a sunny weather in a middle latitude may be only in the daytime.

 

Talking parrot
A thief penetrated into a flat and saw a huge immovable dog and a parrot, sitting  in the cage. The parrot said:
-  You are welcome!
A thief was afraid at the beginning, but then he calmed down, because the dog made nothing. Capturing jewels and money he wanted to go away and asked the parrot at the end:
-  Well, don’t you know other words, foolish bird ?
The parrot answered:
-  Bite him, boy!
+ نوشته شده در چهارشنبه بیست و دوم مهر ۱۳۸۸ ساعت 15:46 توسط عرفان مرادي  | 

Graphical solving of equations

Approximate solution of equations. Graphical solving of
equations in one unknown. Graphical solving of systems
of simultaneous equations in two unknowns.

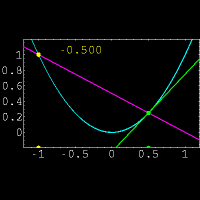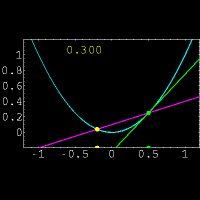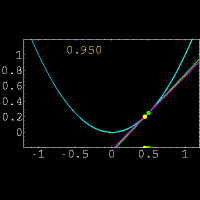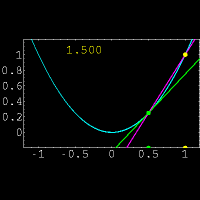
Graphical representation of functions permits to solve approximately any equation in one unknown and a system of two simultaneous equations in two unknowns. To solve a system of two simultaneous equations in two unknowns x and y graphically, we consider each of the equations as a functional dependence between variables x and y and build graphs for these two functions. Coordinates of intersection points of these graphs give us the found values for x and y ( i.e. a solution of this system of simultaneous equations ).

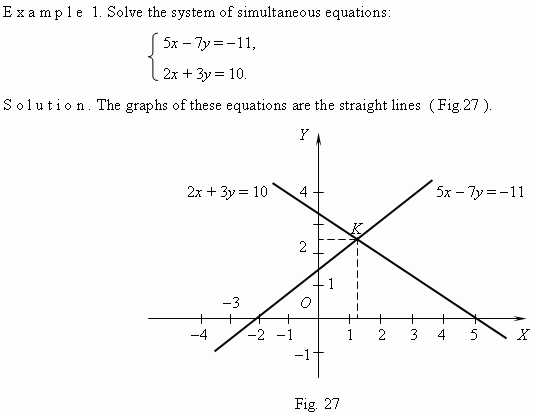
According to these graphs the approximate coordinates of the intersection point K are: x = 1.25,  y = 2.5.  The exact solution of these simultaneous equations is:

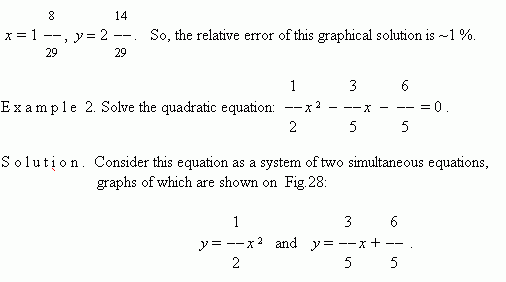
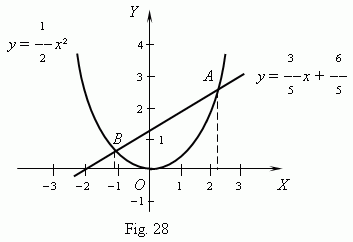
After building the graphs we find abscissas of the intersection points  A and B:
 x1 2.25 ,  x2 –1.1 . Exact values of this equation roots are:

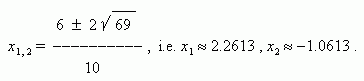
The relative error of the graphical solution in this example is ~3.5 %.

To solve an equation in one unknown graphically, it is necessary to transfer all its terms to the same part, i.e. to reduce it to a shape:

f ( x ) = 0 ,

and to build a graph of the function  y = f ( x ). Abscissas of the graph intersection points with an x-axis will be roots of this equation (zeros of this function).

                     By this graph we find zeros of the function:  x12.25,  x2 –1.1.

+ نوشته شده در چهارشنبه بیست و دوم مهر ۱۳۸۸ ساعت 15:38 توسط عرفان مرادي  | 

Functional dependence between two variables

Functional dependence. Argument ( independent variable ).
Function. Single-valued function. Multiple-valued function.

Two variables x and y are tied by a  functional dependence, if for each value of one of them it is possible to receive by the certain rule one or some values of another.

E x a m p l e . A temperature T of water boiling and atmosphere pressure p are tied by a functional dependence,
because  each value of pressure corresponds to a certain value of the temperature and inversely.
So, if  p = 1 bar, then T = 100°C; if  p = 0.5 bar, then T = 81.6°C.

A variable, values of which are given, is called an argument or an independent variable; the other variable, values of which are found by the certain rule is called a  function. Usually an argument is marked as  x, and a function is marked as  y . If only one value of function corresponds to each value of argument, this function is called a single-valued function; otherwise, if there are many corresponding values, this function is called a multiple-valued function ( two-valued, three-valued and etc.).

E x a m p l e . A body is thrown upwards;  h  is its height over a ground,  t  is the time, passed from a throwing moment.
h is a single-valued function of  t, but  t is a two-valued function of  h, because the body is on the same
height twice: the first time at an assent, the second time at a fall. The formula

binding variables h and  t ( initial velocity  v0 and an acceleration of a gravity g are constants here ), shows that we have only one value of  h at the given t , and two values of  t at the given  h  ( they are determined by solving the quadratic equation )

+ نوشته شده در چهارشنبه بیست و دوم مهر ۱۳۸۸ ساعت 15:35 توسط عرفان مرادي  | 

لیست از سایت های ریاضی جامعه ریاضی آمریکا

 

Contents

 

The resources listed here have been divided into different categories. Please make your selection from the following:

General Mathematics Web Sites in the USA

Go back to Contents . 

General Mathematics Web Sites outside the USA

These entries are listed in alphabetical order of names of the countries. Go back to Contents . 

Pure Mathematics, History of Mathematics and Biographies

Go back to Contents . 

Applied Mathematics, Computational Mathematics and Mathematical Physics

Go back to Contents . 

Math Teaching, Math Education and Math Student Servers

In addtion to the following, you will find material for teaching and education under the Mathematics Software, Books and Publications section of this page. Go back to Contents . 

Statistics, Probability and Related Fields

Go back to Contents . 

Mathematics References, Utilities and FAQ's

Go back to Contents . 

Mathematics Discussion Groups

Go back to Contents . 

Mathematics Newsletters and Announcements

Go back to Contents . 

Mathematics Newsgroups

Go back to Contents . 

Mathematics Software, Programs, Graphers and Calculators

Go back to Contents . 

Mathematics Books and Publications

NOTE: You may search selected libraries or visit web sites of book publishers by linking to our library search / book publishers page .

Go back to Contents . 

Mathematics Journals and Preprints

Go back to Contents . 

Mathematical Art, Graphics,VRML and Cryptography

Go back to Contents . 

College and Pre-College Mathematics -- Activities, Help and Software

Go back to Contents . 

Miscellaneous Web Pages related to Mathematics

+ نوشته شده در جمعه هفدهم مهر ۱۳۸۸ ساعت 18:54 توسط عرفان مرادي  | 

جدول تناوبی توابع

+ نوشته شده در یکشنبه دوازدهم مهر ۱۳۸۸ ساعت 4:1 توسط عرفان مرادي  | 

پیچیده گی های اعداد اول

در150 سال اخیر یا بیشتر نظریه اعداد پیشرفتهای زیادی درجهات مختلف داشته.شرح انواع مسائلی که در نظریه اعداد

بررسی شده اند در اینجا ممکن نیست.این مبحث بسیار وسیع است و در بعضی قسمتها نیاز به دانستن مطالب عمیقی از

ریاضیات پیشرفته (مثل نظریه گالوا و آنالیز در سطح بالا ) دارد. با اینحال مسائل زیادی در نظریه اعداد وجود دارد که به آسانی قابل بیانند . برخی از آنها به اعداد اول مربوط میشوند .

در نوشته ی قبلی اعداد کوچکتر از 500 ذکر شده اند .در 1914 ریاضیدان آمریکایی دی.ان.لمر با منتشر کردن جدول همه اعداد اول کوچکتر از 10 میلیون متوجه شد که فقط 664579 تا عدد اول وجود دارد یعنی حدود6.5 درصد.همچنین دی اچ لمر(پسر دی.ان.لمر) تعداد اعداد اول کوچکتر از 10 میلیارد را حساب

کرد 455052512.حدوداً 4.5 درصد .

بررسی دقیق اعداد اول نشان می دهد که توزیع بسیار نامنظمی دارند . به آسانی ثابت میشود که شکافهای به اندازه ی دلخواه  بین آنها وجود دارد. بررسی این اعداد نشان میدهد که اعداد اول متوالی ، نظیر 3و5 یا 101و103 همین طور تکرار میشوند جفتهایی از اعداد اول که تفاضلشان 2 است اعداد اول دو قلو نامیده میشوند بیش از 1000 جفت از این جفتها زیر 100000  بیش از 8000 جفت زیر 1000000 وجود دارند این مسئله که آیا بینهایت تا از این اعداد وجود دارد یا نه هنوز حل نشده است.

 

سلام  اين اعدادي كه ميبينيد ۵۰۰ تا عدد اول هستش. همينطور كه ميدونيد اعداد اول خيلي پيچيده هستند مثلا شكافهايي به اندازه دلخواه در آنها وجود دارد

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103,107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211,223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331,337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449,457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571,577,587,593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677,683,691, 701, 709,719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853,857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953,967, 971, 977, 983,991,997, 1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069, 1087, 1091, 1093, 1097,1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217,1223,1229, 1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291, 1297, 1301, 1303, 1307, 1319,1321,1327, 1361, 1367, 1373, 1381, 1399, 1409, 1423, 1427, 1429, 1433, 1439, 1447, 1451,1453,1459,1471, 1481, 1483, 1487, 1489, 1493, 1499, 1511, 1523, 1531, 1543, 1549, 1553, 1559, 1567, 1571,1579, 1583, 1597, 1601, 1607, 1609, 1613, 1619, 1621, 1627, 1637, 1657, 1663, 1667, 1669, 1693,1697, 1699, 1709, 1721, 1723, 1733, 1741, 1747, 1753, 1759, 1777, 1783, 1787, 1789, 1801, 1811,1823, 1831, 1847, 1861, 1867, 1871, 1873, 1877, 1879, 1889, 1901, 1907, 1913, 1931, 1933, 1949,1951, 1973, 1979, 1987, 1993, 1997, 1999, 2003, 2011, 2017,2027, 2029, 2039, 2053, 2063,2069,2081, 2083, 2087, 2089, 2099, 2111, 2113, 2129, 2131, 2137,2141, 2143, 2153, 2161, 2179,2203,2207, 2213, 2221, 2237, 2239, 2243, 2251, 2267, 2269,2273,2281, 2287, 2293, 2297, 2309, 2311,2333, 2339, 2341, 2347, 2351, 2357, 2371, 2377,2381,2383, 2389, 2393, 2399, 2411, 2417,2423,2437, 2441, 2447, 2459, 2467, 2473, 2477, 2503, 2521, 2531, 2539, 2543, 2549, 2551, 2557,2579,2591, 2593, 2609, 2617, 2621, 2633, 2647, 2657, 2659, 2663, 2671, 2677, 2683, 2687, 2689,2693,2699, 2707, 2711, 2713, 2719, 2729, 2731, 2741, 2749, 2753, 2767, 2777, 2789, 2791, 2797,2801,2803, 2819, 2833, 2837, 2843, 2851, 2857, 2861, 2879, 2887, 2897, 2903, 2909, 2917,2927,2939,2953, 2957, 2963, 2969, 2971, 2999, 3001, 3011, 3019, 3023, 3037, 3041, 3049, 3061, 3067, 3079,3083, 3089, 3109, 3119, 3121, 3137, 3163, 3167, 3169, 3181, 3187, 3191, 3203, 3209, 3217,3221,3229, 3251, 3253, 3257, 3259, 3271, 3299, 3301, 3307, 3313, 3319, 3323, 3329, 3331, 3343,3347,3359, 3361, 3371, 3373, 3389, 3391, 3407, 3413, 3433, 3449, 3457, 3461, 3463, 3467, 3469,3491,3499, 3511, 3517, 3527, 3529, 3533, 3539, 3541, 3547, 3557, 3559, 3571.

چهل و سومین عدد اول مرسن کشف شد.

در15 دسامبر 2005،بزرگترین عدد اول مرسنی که تا کنون شناخته شده است،کشف گردید. این عدد تقریبا نه میلیون و 150هزار رقمی که به صورت 1-230402457    می باشد و توسط تیمی از دانشگاه میسوری مرکزی ،کشف گردید.

شرکت Frontier foundations  ، براي کشف عدد اول مرسنی كه بیش از 10 میلیون رقم داشته باشد،

 جایزه ای 100000 دلاری تعيين كرده است با این حال این جایزه هنوز دور از دسترس مانده است

 به عددی طبیعی تام میگویند هر گاه مجموع مقسوم علیه های آن برابر دو برابر آن عدد باشند مثلا ۶ تام است

البته می توان ثابت کرد که اگر عددی تام باشد آنگاه مجموع معکوسهای مقسوم علیه های آن عدد برابر ۲ باشد (خیلی ساده هستش خودتون ثابت کنید

گروه سه نفر رياضي دانان هندي براي غلبه بر مشكل به هر دري زدند و با بررسي مقالات مختلف بالاخره دريافتند كه در سال ‪ ۱۹۸۵يك رياضي‌دان فرانسوي به نام اتن فووري از دانشگاه پاريس ‪ ۱۱اين نكته را به صورت رياضي اثبات كرده است. به اين ترتيب آخرين بخش معما حل شد و آلگوريتم پيشنهادي اين سه نفر با موفقيت پا به عرصه گذارد.

اما اين موفقيت "مشروط" بود. به اين معني كه اين روش براي اعداد اولي كه انسان در حال حاضر مي‌توان به سراغ آنها برود از كارآيي چنداني برخوردار نيست. در روايت اوليه روش پيشنهادي، زمان لازم براي محاسبات كه متناسب با ارقام عدد اول مورد نظر بود، با آهنگ ‪ ۱۰۱۲ازدياد پيدا مي كرد.

در روايتهاي بهبود يافته اخير اين روش، سرعت ازدياد زمان لازم براي محاسبات به ‪ ۱۰۷.۵كاهش يافته اما حتي در اين حالت نيز اين روش در مقايسه با روش آ پي آر تنها در هنگامي موثر تر خواهد بود كه تعداد ارقام عدد اولي كه قصد شكار و يافتن آن را داريم در حدود ‪ ۱۰۱۰۰۰باشد.

اعدادي تا اين اندازه بزرگ در حافظه هيچ كامپيوتر جاي نمي‌گيرند و حتي آن را نمي‌توان در كل كيهان جاي داد.

اما حال كه رياضي دانان توانسته‌اند يك طبقه خاص از آلگوريتمهاي تواني را براي شناسايي اعداد اول مشخص كنند، اين امكان پديد آمده كه به دنبال نمونه‌هاي بهتر اين روش بگردند. پومرانس و هندريك لنسترا از دانشگاه كاليفرنيا در بركلي با تلاش در همين زمينه توانسته‌اند زمان لازم براي محاسبات را از توان ‪ ۷.۵به توان ‪ ۶كاهش دهند.

اين دو از همان استراتژي كلي گروه هندي موسسه كانپور استفاده كردند اما تاكتيهاي ديگري را به كار گرفتند.

اگر فرضيه‌هاي ديگري كه درباره اعداد اول مطرح شده درست از كار درآيد آنگاه مي‌توان زمان محاسبه را از توان ‪ ۶به توان ‪ ۳تقليل داد كه در اين حد اين روش كارآيي عملي پيدا خواهد كرد.

در اين حالت يافتن اعداد اول با ‪ ۱۰۰۰رقم يا بيشتر به بازي كودكان بدل خواهد شد.

اما در نظر رياضي‌دانان مهمترين و جالبترين جنبه كار گروه سه نفره آ ك اس (كانپ.ر) روشي است كه آنان به كار گرفته‌اند.

اعداد اول براي رياضيات از اهميت بنيادين برخوردارند و هر نوع غفلت در فهم ويژگيهاي آنها باعث مي‌شود خللهاي بزرگ در بناي رياضيات پديدار شود.

روش اين سه رياضي دان هندي هرچند اين خللها و نقصها را پر نكرده حداقل به رياضي دانان گفته است كه در كجا به دنبال اين خللها بگردند.

آلگوريتم پيشنهادي اين سه محقق و همه انواع بديلي كه بر اساس آن ساخته شده متكي به وجود اعداد اولي با مشخصه هاي ويژه هستند. و در اغلب موارد استفاده از اين روش مستلزم آن است كه رياضي دانان اطلاعات دقيقي از نحوه توزيع اين قبيل اعداد اول خاص در ميان ديگر اعداد به دست آورند و به اين ترتيب جغرافياي مكاني اعداد اول را مشخص سازند.

روش پيشنهادي آ ك اس به رياضي دانان اين نكته را آموخته كه ويژگيهاي اين جغرافياي مكاني حائز اهميت است و نيز اين كه هنوز دانش كافي در اين زمينه به دست نيامده است.

در گذشته و در زماني كه نظريه اعداد تنها مورد توجه يك گروه كوچك از رياضي دانان بود ، اين مساله چندان اهميتي نداشت. اما در ‪ ۲۰سال گذشته اعداد اول موقعيتي استثنايي در عرصه رمز نگاري و دانش طراحي و شكستن رمزها كسب كرده اند.

رمزها صرفا از نظر نظامي و جاسوسي حائز اهميت نيستند بلكه از آنها در عرصه هاي تجاري و نيز فعالييتهاي اينترنتي در مقياس وسيع استفاده به عمل مي‌آيد. هيچ كس نمي‌خواهد كه راهزنان اينترنتي به اطلاعات شخصي مربوط به حسابهاي بانكي يا شماره كارتهاي اعتباري آنان دست يابد.

هم اكنون دزدي مشخصات شناسنامه اي افراد و جعل هويت آنان به صورت يكي از بزرگترين قلمروهاي فعالييتهاي تبهكارانه در سطح بين‌المللي در آمده است.

سازندگان كامپيوترها و ارائه‌دهندگان خدمات اينترنتي با توجه به آنكه در حال حاضر افراد بسياري از فعاليتهاي خود را از طريق اينترنت انجام مي دهند، نظير اينكه پول قبضهاي برق و آب و تلفن خود را مي‌پردازند يا در كلاسهاي مورد نظر ثبت نام مي‌كنند، يا بليت هواپيما و قطار رزرو مي‌كنند، در تلاشند تا از خطر دستيابي تبهكاران به اطلاعات شخصي افراد جلوگيري به عمل اورند.

يكي از مهمترين سيستمهايي كه در اين زمينه مورد استفاده صنايع است سيستم آر اس آ نام دارد كه متكي به اعداد اول است.

اعداد اول مورد استفاده در اين سيستم در حدود ‪ ۱۰۰رقمي هستند. سيستم آر اس آ در بسياري از سيستمهاي كامپيوتري مورد استفاده قرار دارد و در پروتكل اصلي براي ارتباطات امن اينرتنتي نيز گنجانده شده است و بسياري از دولتها، شركتهاي بزرگ و دانشگاهها از آن استفاده مي‌كنند. جواز استفاده از اين سيستم براي بيش از ‪ ۷۰۰شركت صادر شده و بيش از نيم ميليون كپي از آن در سطح جهاني مورد استفاده قرار دارد.

براي شكستن رمز آر اس آ بايد مضراب اعداد ‪ ۲۰۰رقمي يا بزرگتر را پيدا كنيد. هرچند فاكتور گيري يا عامل مشترك گيري از اعداد سخت تر از آزمودن اول بودن آنهاست اما اين دو مساله با يكديگر ارتباط دارند و رياضي دانان از يك ابزار براي حل هر دو مساله استفاده مي‌كنند.

همه اين جنبه‌ها بر اهميت كشف هر روشي براي محاسبه اعداد اول مي‌افزايد.

در سال ‪ ۱۹۹۵زماني كه پيتر شور از آزمايشگاههاي بل اثبات كرد كه مجموعه- اي از آلگوريتمهاي تواني براي فاكتور گيري وجود دارد، لرزه بر اندام بسياري افتاد.

اما خوشبختانه براي استفاده از اين آلگوريتم به كامپيوترهاي كوانتومي نياز است كه هنوز در مرحله تكميل تئوريك قرار دارند.

اكنون روش تازه آگراوال و دوستانش دوباره سيستم آر اس آ را در معرض خطر قرار داده است. آگراوال اكنون اين نكته را نشان داده كه مي‌توان با كامپيوتر هاي معمولي، اعداد را از حيث اول بودن مورد آزمايش قرار داد.

سوالي كه اينك مطرح شده آن است كه آيا الگوريتم مشابهي كه به صورت تواني كار كند براي فاكتورگيري اعداد غيراول نيز موجود است؟ پاسخ اغلب متخصصان به اين پرسش منفي است اما متاسفانه اين متخصصان همين حرف را در مورد آلگوريتم تواني مربوط به اعداد اول نيز مي‌زدند
در حال حاضر رياضي دانان واقعا مطمئن نيستند كه كه آيا چنين آلگوريتمي يافت مي‌شود يا نه.

اگر پاسخ مثبت باشد انگاه سيستم آر اس آ ديگر از امنيت برخوردار نيست.

يك عامل تخفيف‌دهنده نگرانيها آن است كه از سيستم آر اس آ براي انتقال همه محتواي پيامها استفاده نمي‌شود بلكه صرفا "كليد هاي رمز" را كه اندازه شان كوچك است با اين سيستم انتقال مي‌دهند.

براي انتقال بقيه پيام از روشهاي رمزنگاري متعارف بهره گرفته مي‌شود. به اين ترتيب جاسوسان در صدد برخواهند آمد كه به كليد رمزها دست يابند.

به اين ترتيب درسي كه از موفقيت گروه سه نفره هندي گرفته مي‌شود آن است كه بايد با احتياط در ارسال پيامها عمل كرد. اگر اكتشافات مشابه آنچه گروه كانپور بدست اورده تكرار شود، انگاه ديگر نمي‌توان به ايمن بودن ارتباطاتي كه روي اينترنت برقرار مي‌شود اطمينان داشت.

 

 

 

+ نوشته شده در پنجشنبه نهم مهر ۱۳۸۸ ساعت 2:15 توسط عرفان مرادي  | 

آزمايش تامسون ( محاسبه نسبت بار به جرم الکترون )

در آزمايش تامسون از اثر ميدان الکتريکي و ميدان مغناطيسي استفاده شده است. دستگاهي که در اين آزمايش مورد استفاده قرار گرفته است از قسمتهاي زير تشکيل شده است:


<\/h2>

الف ) اطاق يونش که در حقيقت چشمه تهيه الکترون با سرعت معين مي باشد بين کاتد و آند قرار گرفته است. در اين قسمت در اثر تخليه الکتريکي درون گاز ذرات کاتدي ( الکترون ) بوجود آمده بطرف قطب مثبت حرکت مي کنند و با سرعت معيني از منفذي که روي آند تعبيه شده گذشته وارد قسمت دوم مي شود. اگر بار الکتريکي q  تحت تاثير يک ميدان الکتريکي بشدت E  قرار گيرد، نيروييکه از طرف ميدان بر اين بار الکتريکي وارد مي شود برابر است با:      


F= q.E


  چون ذرات الکترون مي باشند q = -e بنابراين:


F= -eE  


از طرف ديگر چون شدت ميدان E  در جهت پتانسيلهاي نزولي يعني از قطب مثبت بطرف قطب منفي است بنابراين جهت نيرويF   در خلاف جهت يعني از قطب منفي بطرف قطب مثبت مي باشد. اگرx  فاصله بين آند و کاتد باشد کار نيروي F در اين فاصله برابر است با تغييرات انرژي جنبشي ذرات . از آنجاييکه کار انجام شده در اين فاصله برابراست با مقدار بار ذره در اختلاف پتانسيل موجود بين کاتد وآند بنابراين خواهيم داشت


ev0 =½m0v2


که در آن  v0    اختلاف پتانسيل بين کاتد و آند e  بار الکترون  v  سرعت الکترون و  m0  جرم آن مي باشد. بديهي است اگر v0  زياد نباشد يعني تا حدود هزار ولت رابطه فوق صدق مي کند يعني سرعت الکترون مقداري خواهد بود که مي توان از تغييرات جرم آن صرفنظ نمود . بنابراين سرعت الکترون در لحظه عبور از آند بسمت قسمت دوم دستگاه برابر است با:


v = ?(2e v0/ m0)


 


ب) قسمت دوم دستگاه که پرتو الکتروني با سرعت v وارد آن مي شود شامل قسمتهاي زير است :


 


 


1- يک خازن مسطح که از دو جوشن  A  وB  تشکيل شده است اختلاف پتانسيل بين دو جوشن حدود دويست تا سيصد ولت مي باشد اگر پتانسيل بين دو جوشن را به v1   و فاصله دو جوشن را به d   نمايش دهيم شدت ميدان الکتريکي درون اين خازن E = v1/d   خواهد بود که در جهت پتانسيلهاي نزولي است.


 


2- يک آهنربا که در دو طرف حباب شيشه اي قرار گرفته و در داخل دو جوشن خازن: يک ميدان مغناطيسي با شدت B  ايجاد مي نمايد . آهنربا را طوري قرار دهيد که ميدان مغناطيسي حاصل بر امتداد ox   امتداد سرعت - و امتداد  oy امتداد ميدان الکتريکي - عمود باشد.



 


پ) قسمت سوم دستگاه سطح دروني آن به روي سولفيد آغشته شده که محل برخورد الکترونها را مشخص مي کند.


وقتي الکترو از آند گذشت و وارد قسمت دوم شد اگر دو ميدان الکتريکي و مغناطيسي تاثير ننمايند نيرويي بر آنها وارد نمي شود لذا مسير ذرات يعني پرتو الکتروني مستقيم و در امتداد ox   امتداد سرعت ) خواهد بود و در مرکز پرده حساس p يعني نقطه  p0 اثر نوراني ظاهر مي سازد.


اگر بين دو جوشن خازن اختلاف پتانسيلv1 را برقرار کنيم شدت ميدان الکتريکي داراي مقدار معين E خواهد بود و نيروي وارد از طرف چنين ميداني بر الکترون برابر است با   FE = e E  اين نيرو در امتداد  oy و در خلاف جهت ميدان يعني از بالا به پايين است.



ميدان مغناطيسي B  را طوري قرار مي دهند که برسرعتv   عمود باشد . الکترون در عين حال در ميدان مغناطيسي هم قرار مي گيرد و نيرويي از طرف اين ميدان بر آن وارد مي شود که عمود بر سرعت و بر ميدان خواهد بود . اگر اين نيرو را بصورت حاصلضرب برداري نشان دهيم برابر است با:


  

FM = q.(VXB)

در اينجا q = e    پس:


FM = q.(VXB)

و مقدار عددي اين نيرو مساوي است با  F = e v B   زيرا ميدان B   بر سرعت v   عمود است يعني زاويه بين آنها 90 درجه و سينوس آن برابر واحد است. اگر ميدان B     عمود بر صفحه تصوير و جهت آن بجلوي صفحه تصوير باشد امتداد و جهت نيروي FM در  جهت  oy يعني در خلاف جهت FE خواهد بود. حال ميدان مغناطيسي B  را طوري تنظيم مي نمايند کهFE = FM  گردد و اين دو نيرو همديگر را خنثي نمايند. اين حالت وقتي دست مي دهد که اثر پرتو الکتروني روي پرده بي تغيير بماند پس در اين صورت خواهيم داشت:


         FM = FE


        e.v.B = e E


        v = E/ B


چون مقدار E و B  معلوم است لذا از اين رابطه مقدار سرعت الکترون در لحظه ورودي به خازن بدست مي ايد . حال که سرعت الکترون بدست آمد ميدان مغناطيسي B  را حذف مي کنيم تا ميدان الکتريکي به تنهاي بر الکترون تاثير نمايد . از آنجاييکه در جهت ox  نيرويي بر الکترون وارد نمي شود و فقط نيروي FE  بطور دائم آنرا بطرف پايين مي کشد لذا حرکت الکترون در داخل خازن مشابه حرکت پرتابي يک گلوله در امتداد افقي مي باشد و چون سرعت الکترون را نسبتا کوچک در نظر مي گيريم معادلات حرکت الکترون ( پرتو الکتروني ) در دو جهت ox و oy  معادلات ديفرانسيل بوده و عبارت خواهد بود از  


m0(d2x /dt2)/span>=0     در امتداox 


  m0d2y /dt2)=e. E      در امتداoy


با توجه به اينکه مبدا حرکت را نقطه ورود به خازن فرض مي کنيم اگر از معادلات فوق انتگرال بگيريم خواهيم داشت:


y=(1/2)(e.E)t2/m0


x=v.t


 معادلات فوق نشان مي دهد  که مسير حرکت يک سهمي است و مقدار انحراف پرتو الکتروني از امتداد اوليه (ox  )  در نقطه خروج از خازن مقدار  y  در اين لحظه خواهد بود . اگرطول خازن را به L  نمايش دهيم x = L    زمان لازم براي سيدن به انتهاي خازن عبارت خواهد بود از t = L / v  اگر اين مقدار  t  را در معادله y   قرار دهيم مقدار انحراف در لحظه خروج از خازن به دست مي آيد:


     Y =  ½ e( E/m0) ( L/ v )2


     e/ m0 = ( 2y/ E ) ( v/ L )2


که در آن v سرعت الکترون که قبلا بدست آمده است. L و E بترتيب طول خازن و شدت ميدان الکتريکي که هر دو معلوم است پس اگر مقدار y را اندازه بگيريم بار ويژه يا e/m0  محاسبه مي شود.


 پس از خروج الکترون از خازن ديگر هيچ نيرويي بر آن وارد نمي شود بنابراين از آن لحظه به بعد حرکت ذره مستقيم الخط خواهد بود و مسير آن مماس بر سهمي در نقطه خروج از خازن است . اگر a  فاصله پرده از خازن يعني D P0 باشد مي توانيم بنويسيم:


P0P1 = y + DP0 tg?


tg?عبارتست از ضريب زاويه مماس بر منحني مسير در نقطه خروج از خازن و بنابراين مقدار يست معلوم پس بايد با اندازه گرفتن فاصله اثر روي پرده( P0 P1)به مقدار y رسيد و در نتيجه مي توانيم e/ m0 را محاسبه نماييم.


مقداري که در آزمايشات اوليه بدست آمده بود 108×7/1 کولن بر گرم بود مقداريکه امروزه مورد قبول است و دقيقتر از مقدار قبلي است برابر 108×7589/1 کولن بر گرم است.


علاوه بر تامسون، ميليکان نيز از سال 1906 تا 1913 به مدت هفت سال با روشي متفاوت به اندازه گيري بار الکترون پرداخت.

+ نوشته شده در شنبه چهارم مهر ۱۳۸۸ ساعت 23:54 توسط عرفان مرادي  | 

اعداد جالب

می خوام چند تا از اعداد جالب رو بهتون معرفی میکنم :

اول: عدد 142857

نگاه کنین ببینین تا وقتی که در اعداد 1تا6 ضربش میکنیم رقم هاش عوض نمیشه:

142857 × 2 =285714
142857 × 3=428571
142857 × 4=571428
142857 × 5=714285
142857 × 6=857142
142857 × 7=999999!!!!

دوم :

اعداد تام (كه مجموع مقسوم عليه هايشان دو برابر خودشان مي شود) هم جالب هستند

براي مثال 2 * 6 = 1 + 2 +3 +6

سوم:

عدد6174

با این ویژگی:
یه عدد 4 رقمی که همه اعداد اون یکسان نباشند رو در نظر می گیریم بعد اعداد اون رو یک بار به طور نزولی و یک بار به طور صعودی مرتب می کنیم و دو عدد بدست اومده رو از هم کم می کنیم.واسه عدد بعدی هم این کارو انجام می دیم،حداکثر بعد از 7 مرحله عدد6174بوجود می یاد که برای این عدد داریم
1467-7641=6174

چهارم :

احتمالا خیلی هاتون این رو دیدین ولی برای اونهایی که ندیدن میگم:
11*11=121
111*111=12321
1111*1111=1234321
11111*11111=123454321
111111*111111=12345654321
1111111*1111111=1234567654321
11111111*11111111=123456787654321
111111111*111111111=12345678987654321
1111111111*1111111111=12345678900987654321
در ضمن شما میتونید باز هم به این اعداد اضافه کنید!!!!!!!!!!!!!!!!!!!!!!!
*=ضرب

 

پنجم :

اعداد خوشحال:

 

یک عدد صحیح مثبت  را در نظر بگیرید. یک دنباله‌ی  تعریف می‌کنیم به‌طوری که  جمع مربعات ارقام  است.

در این صورت n یک «عدد خوشحال» است اگر و فقط اگر i ای وجود داشته باشد به‌طوری که رابطه‌ي ذيل برقرار باشد:





به‌طور مثال 7 یک «عدد خوشحال»است زیرا:



«اعداد خوشحال» (Happy Numbers) کوچک‌تر از 50 عبارت‌اند از:

توجه کنید که اگر یک عدد، «خوشحال»  باشد تمام اعداد ظاهرشده در دنباله‌ی آن نیز «خوشحال»ا‌ند و هم‌چنین اگر ارقام آن را جابه‌جا کنیم عدد حاصل باز «عدد خوشحال» است.

 

اين اعداد هم جالب هستند

 

منبع : سايت همگام www.hamgaam.ir

+ نوشته شده در شنبه چهارم مهر ۱۳۸۸ ساعت 23:44 توسط عرفان مرادي  | 

هندسه نااقليدسى و نسبيت عام اينشتين


در قرن نوزدهم دو رياضيدان بزرگ به نام «لباچفسكى» و «ريمان» دو نظام هندسى را صورت بندى كردند كه هندسه را از سيطره اقليدس خارج مى كرد. صورت بندى «اقليدس» از هندسه تا قرن نوزدهم پررونق ترين كالاى فكرى بود و پنداشته مى شد كه نظام اقليدس يگانه نظامى است كه امكان پذير است. اين نظام بى چون و چرا توصيفى درست از جهان انگاشته مى شد. هندسه اقليدسى مدلى براى ساختار نظريه هاى علمى بود و نيوتن و ديگر دانشمندان از آن پيروى مى كردند. هندسه اقليدسى بر پنج اصل موضوعه استوار است و قضاياى هندسه با توجه به اين پنج اصل اثبات مى شوند. اصل موضوعه پنجم اقليدس مى گويد: «به ازاى هر خط و نقطه اى خارج آن خط، يك خط و تنها يك خط به موازات آن خط مفروض مى تواند از آن نقطه عبور كند.»

هندسه «لباچفسكى» و هندسه «ريمانى» اين اصل موضوعه پنجم را مورد ترديد قرار دادند. در هندسه «ريمانى» ممكن است خط صافى كه موازى خط مفروض باشد از نقطه مورد نظر عبور نكند و در هندسه «لباچفسكى» ممكن است بيش از يك خط از آن نقطه عبور كند. با اندكى تسامح مى توان گفت اين دو هندسه منحنى وار هستند. بدين معنا كه كوتاه ترين فاصله بين دو نقطه يك منحنى است.

هندسه اقليدسى فضايى را مفروض مى گيرد كه هيچ گونه خميدگى و انحنا ندارد. اما نظام هندسى لباچفسكى و ريمانى اين خميدگى را مفروض مى گيرند. (مانند سطح يك كره) همچنين در هندسه هاى نااقليدسى جمع زواياى مثلث برابر با 180 درجه نيست. (در هندسه اقليدسى جمع زواياى مثلث برابر با 180 درجه است.) ظهور اين هندسه هاى عجيب و غريب براى رياضيدانان جالب توجه بود اما اهميت آنها وقتى روشن شد كه نسبيت عام اينشتين توسط بيشتر فيزيكدانان به عنوان جايگزينى براى نظريه نيوتن از مكان، زمان و گرانش پذيرفته شد. چون صورت بندى نسبيت عام اينشتين مبتنى بر هندسه «ريمانى» است. در اين نظريه هندسه زمان و مكان به جاى آن كه صاف باشد منحنى است.

نظريه نسبيت خاص اينشتين تمايز آشكارى ميان رياضيات محض و رياضيات كاربردى است. هندسه محض مطالعه سيستم هاى رياضى مختلف است كه به وسيله نظام هاى اصول موضوعه متفاوتى توصيف شده اند. برخى از آنها چندبعدى و يا حتى nبعدى هستند. اما هندسه محض انتزاعى است و هيچ ربطى با جهان مادى ندارد يعنى فقط به روابط مفاهيم رياضى با همديگر، بدون ارجاع به تجربه مى پردازد. هندسه كاربردى، كاربرد رياضيات در واقعيت است. هندسه كاربردى به وسيله تجربه فراگرفته مى شود و مفاهيم انتزاعى برحسب عناصرى تفسير مى شوند كه بازتاب جهان تجربه اند. نظريه نسبيت، تفسيرى منسجم از مفهوم حركت، زمان و مكان به ما مى دهد. اينشتين براى تبيين حركت نور از هندسه نااقليدسى استفاده كرد. بدين منظور هندسه «ريمانى» را برگزيد.

هندسه اقليدسى براى دستگاهى مشتمل بر خط هاى راست در يك صفحه طرح ريزى شده است اما در عالم واقع يك چنين خط هاى راستى وجود ندارد. اينشتين معتقد بود امور واقع هندسه ريمانى را اقتضا كرده اند. نور بر اثر ميدان هاى گرانشى خميده شده و به صورت منحنى در مى آيد يعنى سير نور مستقيم نيست بلكه به صورت منحنى ها و دايره هاى عظيمى است كه سطح كرات آنها را پديد آورده اند. نور به سبب ميدان هاى گرانشى كه بر اثر اجرام آسمانى پديد مى آيد خط سيرى منحنى دارد. براساس نسبيت عام نور در راستاى كوتاه ترين خطوط بين نقاط حركت مى كند اما گاهى اين خطوط منحنى هستند چون حضور ماده موجب انحنا در مكان - زمان مى شود.

در نظريه نسبيت عام گرانش يك نيرو نيست بلكه نامى است كه ما به اثر انحناى زمان _ مكان بر حركت اشيا اطلاق مى كنيم. آزمون هاى عملى ثابت كردند كه شالوده عالم نااقليدسى است و شايد نظريه نسبيت عام بهترين راهنمايى باشد كه ما با آن مى توانيم اشيا را مشاهده كنيم. اما مدافعين هندسه اقليدسى معتقد بودند كه به وسيله آزمايش نمى توان تصميم گرفت كه ساختار هندسى جهان اقليدسى است يا نااقليدسى. چون مى توان نيروهايى به سيستم مبتنى بر هندسه اقليدسى اضافه كرد به طورى كه شبيه اثرات ساختار نااقليدسى باشد. نيروهايى كه اندازه گيرى هاى ما از طول و زمان را چنان تغيير دهند كه پديده هايى سازگار با زمان - مكان خميده به وجود آيد. اين نظريه به «قراردادگرايى» مشهور است كه نخستين بار از طرف رياضيدان و فيزيكدان فرانسوى «هنرى پوانكاره» ابراز شد. اما نظريه هايى كه بدين طريق به دست مى آوريم ممكن است كاملاً جعلى و موقتى باشند. اما دلايل كافى براى رد آنها وجود دارد؟

+ نوشته شده در شنبه بیست و یکم شهریور ۱۳۸۸ ساعت 17:10 توسط عرفان مرادي  | 

بزرگترین عدد اول جهان

همین پارسال بود که بحث بر سر پیدا کردن اولین عدد اول دنیا با بیش از 10 میلیون رقم بود. حالا که در دسامبر سال 2008 قرار داریم این رکورد شکسته شده است و ....

همین 3 ماه پیش بود ،تاریخ 8 آگوست 2008 ، و باز هم گروه GIMPS

بزرگترین عدد اول حال حاضر دنیا :
1 - ( 43112609 به توان 2 )

تعداد ارقام : 12978189

فکر می کنید حجم این عدد چقدر است :


تعدادی از ارقام ابتدایی و انتهایی این عدد اول :

316470269330255923143453723949
337516054106188475264644140304176732811247493069368692043
185121611837856726816539985465097356123432645179673853590
577238179357900876426103943782376494591742934588497117587
146916972984761159060873250939462085575740754577098620558
011779529884042198287643319330465064455234988142139565785
447474023546353758537324801838120387600868416525400790381
285888256687085855456231577527939305920811766585308670132
129155221804381548625787943020694528015999221718191557761
789038539522349746808797476907664050601248473206874133194
663585334983805734803620705778270910561716767680954814415
310034502440445161332363611749326163346444542332941724120
365148892204420675302563534393044688859445173161934549310
336116821178855375531041423821706430796012246288037483476
218396982916073816451058991831512686327488459585043246778
160788873343661684676258006436582840222063757785048077389
404912747062648672186003349751782781879120470020388873779
589349589877119954283343288199886936593732250320339998610
072339381292833594919318294607585610592445446058872982335
095667132127175014425218125214413231078371985641017807775
785493244577889145039577777188174108486988317893130592966
383813432499006567940128890939479244323108485896276588430
...

((دانلود این عدد32صفحه ای در بخش دانلود ها می باشد))


مشکلی که 2000 سال دانشمندان در پی حل آن بودند , توسط یک ایرانی حل شد !
فرمولی برای محاسبه اعداد اول :







www.eelmi.blogfa.com
+ نوشته شده در پنجشنبه نوزدهم شهریور ۱۳۸۸ ساعت 2:12 توسط عرفان مرادي  | 

نرم افزار رسم نمودار های ریاضی

در این نرم افزار شما با دادن اطلاعات تابع به صورت علائم ریاضی , تابع را آماده و رسم شده برای شما آماده می کند.

www.Ir-Tci.Org


_____________________________________________
 
راهنما :  لینک دانلود این مطلب را از کادر زیر کپی کرده

و بر روی محل تایپ قسمت آدرس مرورگر اینترنتی خود Paste نمائید

و سپس با زدن کلید Enter آن را براحتی دانلود کنید.


حجم فایل : 16 کیلوبایت

پسورد فایل : www.ir-tci.org

+ نوشته شده در دوشنبه شانزدهم شهریور ۱۳۸۸ ساعت 20:25 توسط عرفان مرادي  | 

برنامه رسم نمودار توابع چند جمله ای (بصورت گرافیکی)

همونطور که از اسم پست پیداست ، اینبار برنامه رسم نمودار چند جمله ای ها به زبان سی پلاس پلاس که -از نظر خودم- واقعا جاش بین برنامه های توی اینترنت خالی بود رو نوشتم. این برنامه ساختار خیلی ساده ای داره، و حتما به نظر دوستانی که برنامه کلاس چند جمله ای رو دانلود کردند ، این برنامه کمی آشناست. من این برنامه رو به کمک کلاس چند جمله ای نوشتم. طرز کار با این برنامه هم راحته. در صفحه ابتدای برنامه ، شما باید عدد 1 را وارد کنید تا به قسمت رسم نمودار بروید.در این قسمت باید شما فضایی که تابع می خواهد در آن رسم شود ( ۱=سطح گسترده ۲=متوسط ۳=کوچک ) و سپس کیفیت رسم رو انتخاب کنید.سپس تعداد جملات چند جمله ای رو وارد کرده و سپس به ترتیب پایه ها و توان های جمله های اول تا آخر را وارد کنید.
 به عنوان مثال برای رسم منحنی y=x2-2x+1 ، پس از انتخاب فضا و کیفیت ، تعداد جملات که 3 می باشد را وارد کنید. سپس ابتدا ضریب x2 ، یعنی 1 ، و سپس توان آن یعنی 2 را وارد کنید. بعد بع ترتیب اعداد 2 ، 1 ، 1 و 0 را وارد کنید و کلید Enter را فشار دهید تا برنامه منحنی را برای شما رسم کند.

نمودار y=x رسم شده توسط این برنامه(با کمی تغییر و کاهش اندازه):

نمودار y=x رسو شده توسط برنامه

لازم می دونم که عرض کنم این برنامه توانایی رسم توابعی مانند x-1 رو هم داره ولی در مورد توابع رادیکالی ، مثل تابع x1/5 ، چون توان بصورت ۰.۲ وارد می شود ، تابع x0.2 رسم می شود و این تابع در x های منفی تعریف و رسم نمی شود. در ضمن این برنامه توانایی رسم توابع سینوسی ، کسینوسی ، تانژانت و ... رو نداره ، اما من در حال نشوتن یه برنامه جدید هستم که توانایی رسم توابع سینوس ، کسینوس ، تانژانت ، کتانژانت ، لگاریتم با مبنای ۱۰ و e (عدد نپر)( sin , cos , tan , cot , log10 , ln ) رو داشته باشه. به محض اینکه این برنامه آماده بشه در وبلاگ و برای دانلود می ذارم.

دانلود برنامه رسم نمودار توابع چند جمله ای

+ نوشته شده در دوشنبه شانزدهم شهریور ۱۳۸۸ ساعت 20:21 توسط عرفان مرادي  | 

دانلود نرم افزار ریاضیات

توسط نرم افزار گران قیمت و کارای Algebrator v4.1 شما به راحتی خواهید توانست معادلات و مجهولات پیچیده ریاضی خود را بنویسید و آنها را حل نمایید. فراگیری و مسلط بودن به نرم افزار مربوطه مستلزم به بازه ی زمانی خاصی می باشد که با کمی تمرین و ممارست به آن دست پیدا خواهید کرد. شما هم اکنون می توانید این نرم افزار را به صورت رایگان از سایت ال ایکس ال  دریافت نمائید که امیدواریم مورد پسند و استفاده ی علاقه مندان قرار گیرد.

size : 5 mb

www.lxl.ir :پسوورد

+ نوشته شده در دوشنبه شانزدهم شهریور ۱۳۸۸ ساعت 19:45 توسط عرفان مرادي  | 

مسابقه

تعیین یک عدد حیرت انگیز:

سوال :اگر داشته باشیم cosx=xانگاه عددxرا پیدا کنید.

توضیح:اینجانب در پی مشاهدات وتجربیات خویش در پی چنین معادله ای بودم تا به نتیجه ای رسیدم که می خواستم ببینم کس دیگری هم از این عدد با خبر است یا نه.بدین ترتیب به این عدد جالب وحیرت انگیز دست یافتم واکنون شما خواننده عزیز می توانید هم از طریق ایمیل وهم از طریق نظر در این مسابقه شرکت کنید.                Email:erfan_moradi22@yahoo.com

جایزه:برنده این مسابقه ومسابقات بعدی از یک جزوه المپیاد ریاضی ونمونه سوالات ورودی ازمون دانشگاه واترلو کانادا می باشد که بنده این جایزه را مناسب چنین کسی میدانم.

                                                         www.eelmi.blogfa.com

+ نوشته شده در دوشنبه شانزدهم شهریور ۱۳۸۸ ساعت 3:25 توسط عرفان مرادي  |