مشتق گیری و مشتق پذیری
مشتق گیری و مشتق پذیری :
در گذشته های نه چندان دور، مشتق یک تابع را به صورت زیر نشان می دادند:
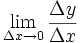
که در این فرمول
 نشان دهنده میزان تغییرات یک کمیت است. ولی در حال حاضر برای محاسبه مشتق توابع،بیشتر از فرمول زیر استفاده میکنند:
نشان دهنده میزان تغییرات یک کمیت است. ولی در حال حاضر برای محاسبه مشتق توابع،بیشتر از فرمول زیر استفاده میکنند: 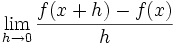
معمولا از نمادهای زیر برای نشان دادن مشتق تابع f نسبت به متغیر x، استفاده میکنند:
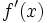 |
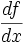 |
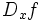 |
یک تابع را در نقطه ای مانند x مشتق پذیر گویند اگردر آن نقطه مشتق موجود باشد. و برای مشتق پذیری تابع در یک بازه لازم است تابع در هر نقطه دلخواه از بازه مشتق پذیر باشد.اگر تابع در نقطه ای مانند c پیوسته نباشد آنگاه در c نمیتواند مشتق پذیر باشد.البته لازم به ذکر است که پیوستگی در یک نقطه وجود مشتق را تضمین نمیکند.مشتق یک تابع مشتق پذیر میتواند خود نیز مشتق پذیر باشد،که به مشتق آن مشتق دوم تابع گویند.مشتق مراتب بالاتر نیز به همین ترتیب تعریف میشوند.
بررسی مشتق از نظر هندسی :
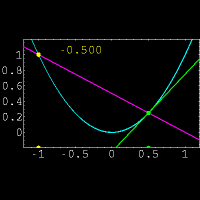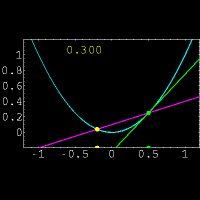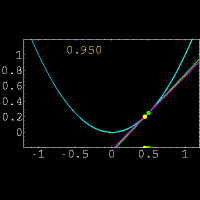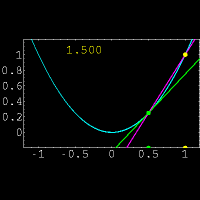 |
از نظر هندسی مشتق یک تابع در یک نقطه دلخواه ،شیب خط مماس بر منحنی در آن نقطه است.البته پیدا کردن مستقیم شیب خط مماس در یک نقطه کار دشواری است.زیرا فقط مختصات یک نقطه از خط مماس را داریم.(برای پیدا کردن شیب یک خط از مختصات دو نقطه بر روی خط استفاده میکنیم)برای حل این مشکل از یک خط متقاطع استفاده کرده و این خط را به خط مماس نزدیک میکنیم.برای درک بهتر موضوع به شکل مقابل توجه نمایید.در این شکل خط متقاطع با رنگ بنفش و خط مماس با رنگ سبز مشخص شده است و عددی که در تصویر تغییر میکند نشان دهنده شیب خط متقاطع میباشد. حال از دیدگاه ریاضی این روش را بیان میکنیم:
از دیدگاه ریاضی بدست آوردن مشتق با حد گیری از شیب خط قاطع که به خط مماس نزدیک شده است بدست می آید.پیدا کردن شیب نزدیکترین خط متقاطع به خط مماس با استفاده از کوچکترین h در فرمول زیر حاصل میشود:
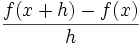
| عکس پیدا نشد |
|
|
در این فرمول h به عنوان کوچکترین تغییر متغیر x تعریف میشودو میتواند مقدار مثبت یا منفی اختیار کند. در این فرمول شیب خط با استفاده از نقاط
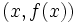 و
و 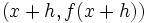 حاصل میشود.واضح است که در این روش فقط یک نقطه روی خط برای ما معلوم است
و نیازی برای بدست آوردن نقطه دوم روی خط وجود ندارد.همچنین در این روش
مشتق x ،حاصل حد زیر است:
حاصل میشود.واضح است که در این روش فقط یک نقطه روی خط برای ما معلوم است
و نیازی برای بدست آوردن نقطه دوم روی خط وجود ندارد.همچنین در این روش
مشتق x ،حاصل حد زیر است: 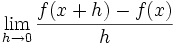
ارتباط مشتق با علم فیزیک :
نقاط بحرانی :
تجزیه و تحلیل نمودارها :
مشتق ابزار مناسبی برای آزمودن نمودار تابع است. نقاطی از دامنه تابع
که به ازای آنها مشتق اول برابر صفر شود میتوانند نقاط اکسترمم نسبی تابع
باشند.البته باید توجه کرد که تمام نقاط بحرانی نقاط اکسترمم نسبی
نیستند.برای مثال تابع 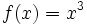 یک نقطه بحرانی در x=0 دارد، ولی میتوان از نمودار تابع متوجه این نکته شد که تابع در این نقطه دارای ماکزیمم یا مینیمم نسبی نیست.
یک نقطه بحرانی در x=0 دارد، ولی میتوان از نمودار تابع متوجه این نکته شد که تابع در این نقطه دارای ماکزیمم یا مینیمم نسبی نیست.
آزمون مشتق اول و آزمون مشتق دوم
، روش هایی را برای تشخیص نقاط ماکزیمم و مینیمم نسبی فراهم میکند.لازم به
ذکر است در فضاهای چند بعدی نقاط اکسترمم را با استفاده از مشتقات جزئی بدست میآورند.
رسم خم با استفاده از مشتق اول:
وقتی بدانیم که تابعی در هر نقطه از بازهای مشتق دارد، بنابر قضایای
مشتق خواهیم دانست که تابع در سراسر آن بازه پیوسته است و نمودارش در آن
بازه قطع شدگی ندارد. مثلا نمودارهای توابع مشتقپذیر y=Sin x همانند نمودار چند جملهایها ، هر چه ادامه بیابند قطع نمیشوند. نمودارهای y = tan x و y = 1/x2
صرفا در نقاطی که توابع مربوط تعریف نشده هستند قطع میشوند. بر بازهای
که این نقاط را شامل نباشند توابع مزبور مشتق پذیرند؛ و بنابراین
پیوستهاند و نمودارهایشان قطع شدگی ندارد. اگر بدانیم مشتق تابعی کجا
مثبت و کجا منفی و کجا صفر میباشد، آنگاه میتوانیم درباره شکل نمودار آن
تابع اطلاعاتی بدست آوریم. با دانستن این مطلب میتوان مشخص کرد که نمودار
در کجا بالا میرود ، پایین میآید یا مماس افقی دارد.
تایعی چون (y = f(x
را سراسر یک بازه Iصعودی میگویند. هرگاه با افزایش y , x هم زیاد شود ؛ و
در سراسر I نزولی گویند هرگاه با افزایش x و y کاهش یابد. وقتی x در I از
چپ به راست حرکت میکند نمودار یک تابع صعودی ، خیز بر میدارد و نمودار
یک تابع نزولی افت میکند. صعود یک تابع با مشتقهای مثبت همراه است و نزول
تابع با مشتقهای منفی. بنابراین اگر ´f در هر نقطه از یک بازه I مثبت لاشد
آنگاه f بر I صعود می کند. و اگر ´f در هر نقطه I منفی باشد، آنگاه f بر I
نزول میکند. این واقعیتها را به عنوان آزمون مشتق اول برای صعودی و نزولی
بودن میپذیریم. آزمون مشتق اول به زبان هندسی حاکمی است که توابع
مشتقپذیر بر بازههایی صعود میکنند که نمودارشان شیب مثبت داشته باشند و
بر بازههایی نزول می کنند که نمودارشان شیب منفی داشته باشند.
مماسهای افقی:
از آنجا که مشتقی چون ´f در هر بازه I یی که َf تعریف شود دارای ویژگی مقدار میانی است، هر وقت ´f در این بازه تغییر علامت میدهد، باید مقدارش صفر شود. پس هر وقت َf در بازه I تغییر علامت میدهد نمودار f باید مماس افقی داشته باشد. اگر وقتی x از چپ به راست میرود و از نقطهای چون C میگذرد، مقدار ´f از مثبت به منفی تبدیل شود، آنگاه مقدار f در c یک مقدار Max موضعی f است. به همین ترتیب اگر وقتی x از از چپ به راست حرکت میکند و از نقطهای چون d میگذرد. مقدار ´f از منفی به مثبت تبدیل شود. مقدار f در d یک مقدار Min موضعی f است. *نمیتوان گفت که هر وقت مشتق صفر شد الزاما تغییر علامت در نمودار تابع ایجاد میشود، بنابراین گاهی اوقات در حالی که Min , Max وجود ندارند مماس افقی وجود دارد، مثل تابع y = x3 با اینکه y´= 3x2 در مبدأ صفر است و در هر دو طرف مثبت است. با این همه مماس افقی y=0 نمودار y = x3 را در مبدأ قطع میکند.
تقعر و نقطه عطف:
در این قسمت چگونگی رسم دقیقتر نمودار با استفاده از علامت مشتق دوم تابع را تشریح میکنیم. همان طور که میدانیم تابع y = x3 (برای خودتان رسم کنید) همراه با افزایش x صعود میکند. اما قسمتی از خم که مربوط به بازه (0, ∞-) و قسمت مربوط به (∞و0) در جهتهای متنفاوتی میپیچیند، اگر در امتداد خم از سمت چپ به طرف مبدأ برویم پیچش خم به سمت راست است. وقتی از مبدأ دور میشویم، خم به سمت چپ میپیچد. توصیف پیچش به طریق دیگر این است که وقتی نقطه تماس از سمت چپ به مبدأ میل میکند مماس بر خم در جهت ساعت میچرخد، در این حالت شیب خم تقلیل مییابد. وقتی نقطه تماس از مبدأ وارد ربع اول میشود، مماس در خلاف جهت ساعت میچرخد. در این حالت میگوییم شیب خم زیاد شده است. بنابراین برای یافتن روی تقعر توسط مشتق باید بگوییم در بازهای که ´y کم میشود تقعر رو به پایین دارد و در بازهای که ´y زیاد میشود تقعر رو به بالا دارد. توسط آزمون مشتق دوم میتوانیم بگوییم در نمودار (y = f(x ، در بازهای که مشتق دوم y کوچکتر از صفر باشد، تقعر رو به پایین دارد. در بازه ای که مشتق دوم y بزرگتر از صفر باشد، تقعر رو به بالا دارد.
کاربرد نقطه عطف در رسم توابع :
نقطهای از خم که در آن تقعر عوض میشود نقطه عطف داریم. پس نقطه عطف خمی که دو بار مشتق پذیر است نقطهای است در یک طرفش مثبت و در طرف دیگرش منفی است و خود مشتق دوم y در نقطه عطف مقدار صفر دارد. البته ممکن است مشتق دوم y در نقطهای که عطف نیست صفر باشد. همچنین ممکن است نقطه عطف در جایی باشد که مشتق دوم y وجود نداشته باشد.
مجانبها و تقارن :
در این قسمت توابع گویا از x را با در نظر گرفتن رفتارشان ، وقتی مخرج
به صفر نزدیک یا x از لحاظ عددی بزرگ میشود، بررسی می کنیم. نمودار تابع
های زوج وفرد تقارنهایی دارند که آگاهی از آنها برای ترسیم نمودارشان مفید
و مهم است.
- باید این را بدانیم که نمودار توابع زوج نسبت به محور yها متقارن است و نمودار توابع فرد نسبت به مبدأ مختصات متقارن میباشد.
مجانبهای افقی و قائم :
وقتی یک نقطه p روی نمودار تابعی چون (y = f(x رفته رفته از
مبدأ دور میشود، ممکن است فاصله بین p و خطی ثابت به صفر نزدیک شود؛ به
عبارت دیگر ، خم وقتی از مبدأ دور میشود به خط میل کند. در این حالت ، خط
را مجانب نمودار مینامند.
خط y = b مجانب افقی نمودار (y = f(x است اگر داشته باشیم: حد تابع (y = f(x وقتی که x به سمت بینهایت و یا منفی بینهایت میل میکند برابر با b شود.
خط x = a مجانب قائم نمودار تابع است، اگر داشته باشیم: حد تابع (y = f(x وقتی که x به سمت a- و یا a+ میل میکند برابر با ∞± شود.
مجانب مایل :
اگر تابع گویایی خارج قسمت دو چند جملهای باشد که عامل مشترک نداشته باشند و اگر درجه صورت ، یک واحد از درجه مخرج بیشتر باشد، آنگاه نمودار یک مجانب مایل دارد. و بطور کلی برای رسم نمودار یک تابع باید مجانبها ، تقعرها ، نقاط عطف ، مماسها ، نقاط اکسترمم باید مشخص باشند.
کاربردها :
رسم توابع مورد بحث ما در جاهای بسیار وسیع کاربرد دارد. برای مثال پرتاب یک موشک یا یک سفینه با بدست آوردن توابع مربوط و رسم نمودار آ«ها توسط کامپیوتر قبل از عملیات پرتاب توسط مهندسین مورد بررسی قرار میگیرد تا نحوه حرکت و سایر موارد مو شکافی گردد. در ستاره شناسی ، مکانیک ، شیمی و حتی علوم انسانی رسم نمودار توابع از ارزش اجتناب ناپذیری برخوردار است.
اکسترمم:
اگر تابع 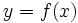 در فاصله ی
در فاصله ی  تعریف شده باشد، آنگاه نقطه ی
تعریف شده باشد، آنگاه نقطه ی  از نقاط داخلی این فاصله رایک نقطه ی ماکزیمم (یا یک نقطه ی مینیمم) تابع
از نقاط داخلی این فاصله رایک نقطه ی ماکزیمم (یا یک نقطه ی مینیمم) تابع 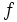 گویند، اگر همسایگی این نقطه مانند
گویند، اگر همسایگی این نقطه مانند  وجود داشته باشد به طوری که برای هر
وجود داشته باشد به طوری که برای هر  در این فاصله، نامساوی
در این فاصله، نامساوی  (یا
(یا  ) برقرار باشد. نقاط ماکزیمم و مینیمم تابع را نقاط حد نهایی یا نقاط اکسترمم تابع می گویند.
) برقرار باشد. نقاط ماکزیمم و مینیمم تابع را نقاط حد نهایی یا نقاط اکسترمم تابع می گویند.
شرط لازم وجود اکسترمم :
در نقاط اکسترمم مشتق صفر است و یا وجود ندارد.
توجه: نقاطی که در آن ها  یا وجود نداشته باشد را نقاط بحرانی گویند.
یا وجود نداشته باشد را نقاط بحرانی گویند.
شرط های کافی وجود اکسترمم :
- چنانچه تابع
 در همسایگی از
در همسایگی از  پیوسته باشد:
پیوسته باشد:
- اگر وقتی
 ،
،  و وقتی
و وقتی  ،
،  (یعنی زمانی که از طرف چپ به طرف راست نقطه ی
(یعنی زمانی که از طرف چپ به طرف راست نقطه ی  حرکت کنیم، علامت مشتق از مثبت به منفی تبدیل شود)، آنگاه
حرکت کنیم، علامت مشتق از مثبت به منفی تبدیل شود)، آنگاه  نقطه ی ماکزیمم است.
نقطه ی ماکزیمم است.
- اگر وقتی
 ،
،  و وقتی
و وقتی  ،
،  (یعنی در حرکت از طرف چپ به طرف راست نقطه ی
(یعنی در حرکت از طرف چپ به طرف راست نقطه ی  ، علامت مشتق از منفی به مثبت تبدیل شود)، آنگاه
، علامت مشتق از منفی به مثبت تبدیل شود)، آنگاه  را نقطه ی مینیمم گویند.
را نقطه ی مینیمم گویند.
- اگر علامت مشتق در دو طرف نقطه ی
 ثابت بماند، آنگاه این نقطه اکسترمم نیست.
ثابت بماند، آنگاه این نقطه اکسترمم نیست.
- اگر وقتی
- چنانچه تابع
 در نقطه ی بحرانی
در نقطه ی بحرانی  دوبار مشتق داشته باشد، اگر
دوبار مشتق داشته باشد، اگر  ، آنگاه تابع در نقطه ی
، آنگاه تابع در نقطه ی  ماکزیمم دارد و اگر
ماکزیمم دارد و اگر  ، آنگاه
، آنگاه  مینیمم تابع است ولی اگر
مینیمم تابع است ولی اگر  ، در این حالت موجودیت اکسترمم در نقطه ی مذکور معلوم نیست.
، در این حالت موجودیت اکسترمم در نقطه ی مذکور معلوم نیست.
- جنانجه
 ولی
ولی  ، اگر
، اگر  زوج باشد، آنگاه وقتی
زوج باشد، آنگاه وقتی  تابع در
تابع در  ماکزیمم است و وقتی
ماکزیمم است و وقتی  تابع در این نقطه مینیمم است. حال اگر
تابع در این نقطه مینیمم است. حال اگر  فرد باشد، آنگاه در نقطه ی
فرد باشد، آنگاه در نقطه ی  اکسترمم وجود ندارد.
اکسترمم وجود ندارد.
- چنانچه تابع
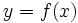 با معادلات پارامتری
با معادلات پارامتری  مشخص شده باشد که در آن
مشخص شده باشد که در آن  در فاصله ی تغییرات متغییر
در فاصله ی تغییرات متغییر 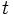 مشتقات مرتبه ی اول و دوم دارند و
مشتقات مرتبه ی اول و دوم دارند و  ، به علاوه در
، به علاوه در  ،
،  آنگاه:
آنگاه:
- اگر
 آنگاه تابع
آنگاه تابع 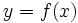 در
در  ماکزیمم دارد.
ماکزیمم دارد.
- اگر
 آنگاه تابع
آنگاه تابع 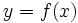 در
در  مینیمم دارد.
مینیمم دارد.
- اگر
 ، در این حالت موجودیت اکسترمم در این نقطه معلوم نیست.
، در این حالت موجودیت اکسترمم در این نقطه معلوم نیست.
- اگر
محاسبه ی بیشترین و کمترین مقدار تابع :
بیشترین (یا کمترین) مقدار تابع پیوسته ی  در فاصله ی
در فاصله ی 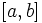 یا در نقاط بحرانی و یا در نقاط انتهایی فاصله است. برای تعیین بیشترین
(یا کمترین) مقدار تابع، مقدار آن در تمام نقاط بحرانی واقع در فاصله ی
یا در نقاط بحرانی و یا در نقاط انتهایی فاصله است. برای تعیین بیشترین
(یا کمترین) مقدار تابع، مقدار آن در تمام نقاط بحرانی واقع در فاصله ی 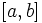 ، و مقادیر
، و مقادیر  را حساب می کنیم و سپس بیشتری (یا کمترین) مقدار بین آن ها را انتخاب می کنیم.
را حساب می کنیم و سپس بیشتری (یا کمترین) مقدار بین آن ها را انتخاب می کنیم.
اگر فاصله ای که تابع در آن تعریف شده است فاصله ی باز باشد، ممکن است تابع بیشترین (یا کمترین) مقدار نداشته باشد.
 وبلاگي از شهرستان ساوه
وبلاگي از شهرستان ساوه